Алгебра, вопрос задал gak81 , 6 лет назад

Напишите пожалуйста ответ письменно. Номер 8.4 буквы а), б), в), г). Задание разложить на множители.

Приложения:

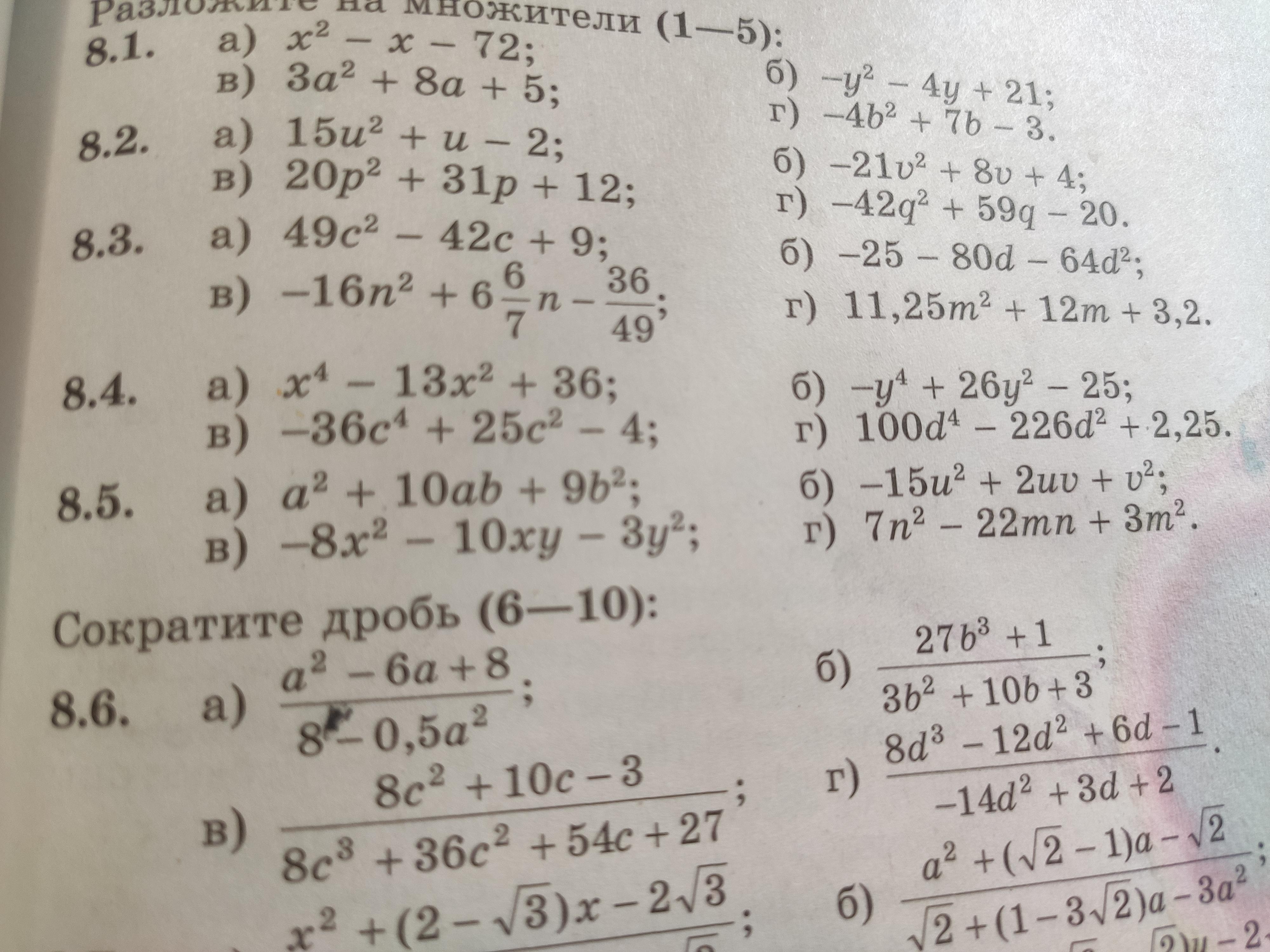
Ответы на вопрос

Ответил LymarIvan

Ответ:

а) (x-3)(x-2)(x+2)(x+3)

б) (5-y)(y-1)(y+1)(y+5)

в) (2-3c)(2c-1)(2c+1)(3c+2)

г) (5d-0.5)(2d-3)(2d+3)(5d+0.5)

Объяснение:

а)

$x^4-13x^2+36=\bigg((x^2)^2-2*6x^2+6^2\bigg)-x^2=\\(x^2-6)-x^2=(x^2-x-6)(x^2+x-6)=\\(x-3)(x+2)(x-2)(x+3)$

б)

$-y^4+26y^2-25=-(y^4-26y^2+25)=-\bigg(\big((y^2)^2-2*5y^2+5^2\big)-16y^2\bigg)=\\-\bigg((y^2-5)^2-(4y)^2\bigg)=-\bigg((y^2-4y-5)(y^2+4y-5)\bigg)=\\-\bigg((y-5)(y+1)(y-1)(y+5)\bigg)=(5-y)(y+1)(y-1)(y+5)$

В первых двух примерах я находил корни квадратных трехчленов на последнем шаге по теореме Виета.

в)

$-36c^4+25c^2-4=-(36c^4-25c^2+4)=-\bigg(\big((6c^2)^2-2*6c^2*2+2^2)\big)-c^2\bigg)=\\-\bigg((6c^2-2)^2-c^2\bigg)=-\bigg((6c^2-c-2)(6c^2+c-2)\bigg)=$

$\begin{bmatrix}6c^2-c-2=0\\D=b^2-4ac=(-1)^2+4*6*2=1+48=49\\c=\frac{-b\pm\sqrt{D} }{2a}\\c_1=\frac{1+\sqrt{49} }{6*2}=\frac{1+7}{12}=\frac{2}{3}\\c_2=\frac{1-\sqrt{49} }{6*2}=\frac{1-7}{12}=-\frac{1}{2} \end{bmatrix}\\\begin{bmatrix}6c^2+c-2=0\\D=b^2-4ac=1^2+4*6*2=1+48=49\\c=\frac{-b\pm\sqrt{D} }{2a}\\c_1=\frac{-1+\sqrt{49} }{6*2}=\frac{-1+7}{12}=\frac{1}{2}\\c_2=\frac{-1-\sqrt{49} }{6*2}=\frac{-1-7}{12}=-\frac{2}{3} \\\\\end{bmatrix}$

$=-\bigg(6(c-\frac{2}{3})(c+\frac{1}{2})*6(c-\frac{1}{2})(c+\frac{2}{3})\bigg)=\\-\bigg((3c-2)(2c+1)(2c-1)(3c+2)\bigg) =(2-3c)(2c+1)(2c-1)(3c+2)$

г)

$100d^4-226d^2+2.25=\bigg((10d^2)^2-2*10d^2*1.5+1.5^2\bigg)-196d^2=\\(10d^2-1.5)^2-(14d)^2=(10d^2-14d-1.5)(10d^2+14d-1.5)=$

$\begin{bmatrix}10d^2-14d-1.5=0\\D=b^2-4ac=(-14)^2+4*10*1.5=196+60=256\\d=\frac{-b\pm\sqrt{D} }{2a}\\d_1=\frac{14+\sqrt{256} }{10*2}=\frac{14+16}{20}=1.5\\d_2=\frac{14-\sqrt{256} }{10*2}=\frac{14-16}{20}=-0.1\end{bmatrix}\\\begin{bmatrix}10d^2+14d-1.5=0\\D=b^2-4ac=14^2+4*10*1.5=196+60=256\\d=\frac{-b\pm\sqrt{D} }{2a}\\d_1=\frac{-14+\sqrt{256} }{10*2}=\frac{-14+16}{20}=0.1\\d_2=\frac{-14-\sqrt{256} }{10*2}=\frac{-14-16}{20}=-1.5\end{bmatrix}$

$=10(d-1.5)(d+0.1)*10(d-0.1)(d+1.5)=(2d-3)(5d+0.5)(5d-0.5)(2d+3)$

Предыдущий вопрос

Следующий вопрос

Новые вопросы

Математика, 1 год назад

площадь классной доски прямоугольной формы 288 кв дм , а её длина 24 дм. Найди ширину доски.

Другие предметы, 1 год назад

Очень срочно!!! Помогите, пожалуйста!!! Нужно подготовить убедительное рассуждение для объяснения написания слов "пруд замёрз", "военный парад". Почему слово пруд пишется с буквой "д", слово замёрз -...

Английский язык, 6 лет назад

13.Write the sentences a) in the negative b) in the interrogative...

Русский язык, 6 лет назад

напишите какова роль обращений в поэтической речи.ответ должен быть полным.

Математика, 8 лет назад

составь равенство в котором делимое и значение частного - четырехзначные числа...

Математика, 8 лет назад

плизз порошуу я вас напишите упражнение N 776.(страница 83).Дам 10 балл срочно надо...