Напишите функцию fibBinet(n), которая будет вычислять Fn по формуле Бине, согласно которой Fn равно ближайшему целому для ϕn/√5, где ϕ=(1+√5)/2 – золотое сечение. Проверьте её для значения F77 (должно получиться fibBinet(77) = 5527939700884757).

Формула Бине:

При работе с типом double имеет место быть некоторая погрешность. При больших числах относительная погрешность стремится к 0.

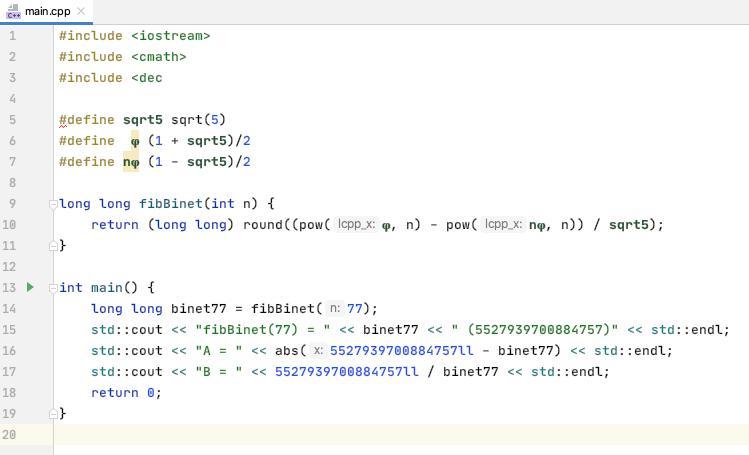
Код:

• #include <iostream>
• #include <cmath>
• #define sqrt5 sqrt(5)
• #define   (1 + sqrt5)/2
• #define n (1 - sqrt5)/2
• long long fibBinet(int n) {
•    return (long long) round((pow(, n) - pow(n, n)) / sqrt5);
• }
• int main() {
•    long long binet77 = fibBinet(77);
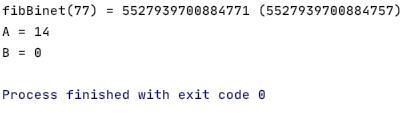
•    std::cout << "fibBinet(77) = " << binet77 << " (5527939700884757)" << std::endl;
•    std::cout << "A = " << abs(5527939700884757ll - binet77) << std::endl;
•    std::cout << "B = " << 5527939700884757ll / binet77 << std::endl;
•    return 0;
• }