Написать уравнение касательной к графику функции
y  f (x)
в точке с абсциссой
x0  a
и построить графики функции
y  f (x)
и найденной касательной.
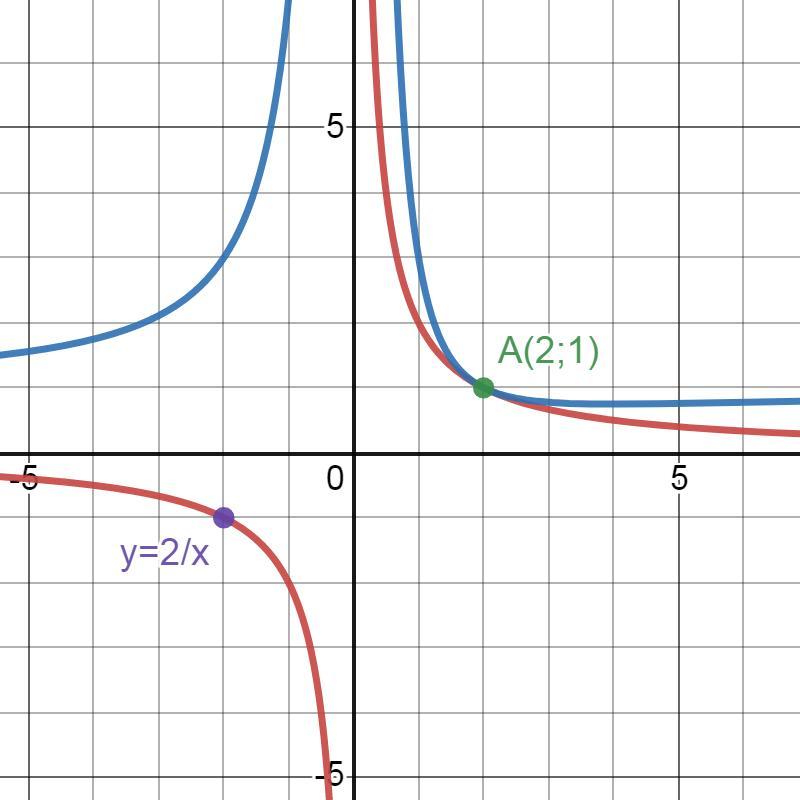
y=2/x a=2

Ответ:

x²-2x-48=0

D= 4+192=196

x1= (2-14)/2= -6

x2= (2+14)/2= 8

8-(-6)= 8+6= 14

mitgliedd1 и 6 других пользователей посчитали ответ полезным!

СПАСИБО

5

5,0

(1 оценка)

Разблокированный значок показывает две руки складывающиеся в форму сердца на фоне розового круга

Нашел этот

Объяснение: