НАДЕЮСЬ НА ВАШУ ПОМОЩЬ!
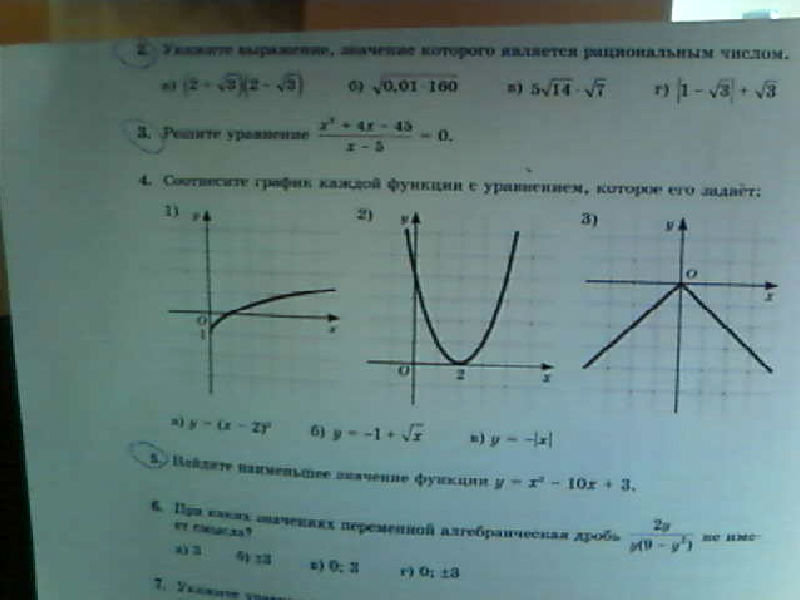
№2. укажите выражение, значение которого является иррациональным числом.
№3 решите уравнение.
№5 найдите наименьшее значение функции.
Прошу вас, помогите всего три номера. номер 3 и 5 с решением. НАДЕЮСЬ НА ВАШУ ПОМОЩЬ!

1)
Скобки спокойно сворачиваются по формуле разности квадратов
Подходит.

Рациональный корень не извлекается. Не подходит.

Рациональный корень не извлекается. Не подходит.

Корень из трёх - приблизительно 1.7. Значит, под модулем отрицательное число. Меняем знак на противоположный и убираем знак модуля (поскольку из-под модуля выходит всегда неотрицательное число)

Рациональный корень опять не извлекается.
Ответ: 1.
2)Плохо видно. Предполагаю, это

Область допустимых значений/ОДЗ/ограничение на х (не знаю как у вас принято это обозначать) - знаменатель неравен нулю, т.е.
x - 5 ≠ 0
x ≠ 5
Затем умножаем обе части уравнения на (х-5)

Первый корень не удовлеторяет ограничению на x, следовательно корень уравнения: х = -9
Ответ: х = -9.
3. Графиком функции

является парабола, ветви которой направлены вверх (т.к. как старший коэффициент положителен). Следовательно, наименьшее значение находится в вершине параболы.
х0, ордината точки, в которой находится парабола, ищется по формуле:

т.е.
х0 = 10/2 = 5.
Но нам нужно само значение функции, поэтому мы ищем y0, которое ищется как:

подставляем найденное нами х0 в функцию, находим у0
y0 = 25 - 50 + 3 = -22
Ответ: -22

Да, все совпадает, спасибо Вам огромное)

пожалуйста:)