На стороне BC ромба ABCD выбрана точка K так, что AK=BD. Оказалось, что ∠KAD=3∠BDK. Найдите угол ABC

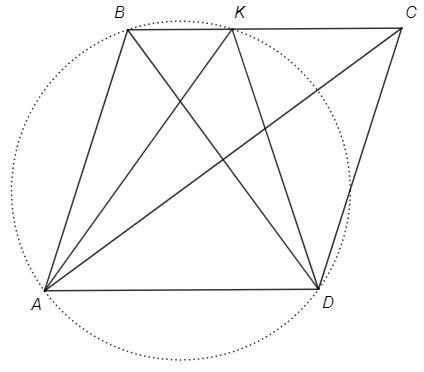
Противоположные стороны параллелограмма параллельны, ABKD - трапеция.

Диагонали равны (AK=BD) - трапеция равнобедренная.

Равнобедренную трапецию можно вписать в окружность.

Вписанный угол равен половине дуги, на которую опирается.

∠KAD=∪KD/2

∠BDK=∪BK/2

∠BDK=∠KAD/3 => ∪BK =∪KD/3

Смежные стороны ромба равны, AB=AD.

Боковые стороны равнобедренной трапеции равны, AB=KD.

Равные хорды стягивают равные дуги.

∪AB=∪AD=∪KD

∪AB+∪BK+∪KD+∪AD =360 => 10/3 ∪KD =360 => ∪KD=108

∠ABK =(∪AD+∪KD)/2 =∪KD =108