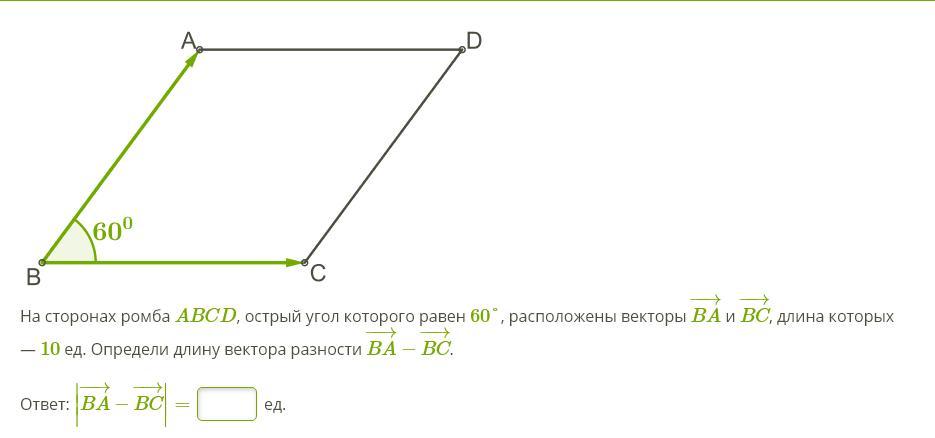
На сторонах ромба ABCD, острый угол которого равен 60°, расположены векторы BA и BC, длина которых — 10 ед. Определи длину вектора разности BА − BC.

Ответ: BA−BC=? ед.

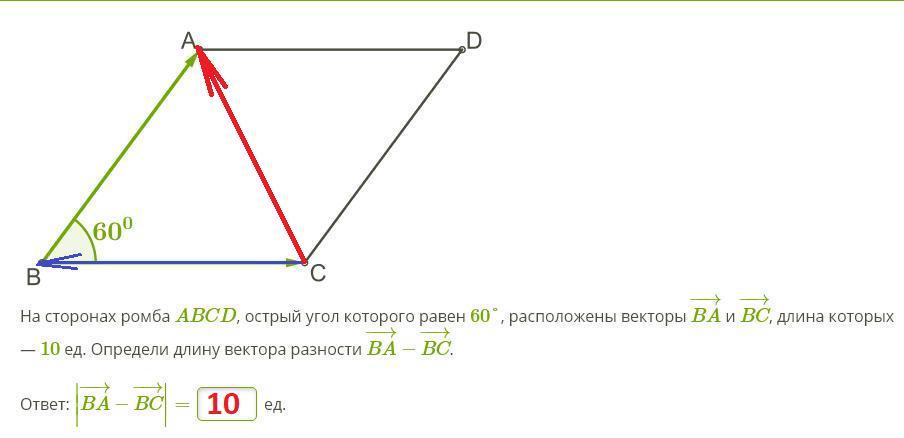
Дано : ABCD,  BA = BC = CD = AD = 10 ед,

          ∠B = ∠D = 60°

Найти :

Решение :

Сложение векторов по правилу треугольника

То есть по условию нужно найти длину диагонали CA.

BA = BC    ⇒   ΔABC - равнобедренный

⇒  ∠CAB = ∠ACB = (180° - 60°) : 2 = 60°

⇒  ΔABC - равносторонний

⇒  CA = BA = BC = 10 ед