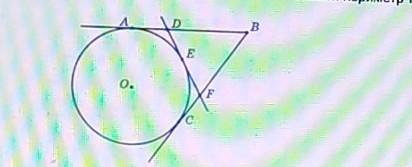
На рисунку точка О центр кола радіуса R; BA BC, DF дотичні до кола (точки А, С, Е точки дотику відповідно): AB = 30 см. Знайти периметр трикутника DBF
​

Ответ:

Периметр трикутника DBF дорівнює 60 см

Объяснение:

На рисунку точка О центр кола радіуса R; BA BC, DF дотичні до кола (точки А, С, Е точки дотику відповідно): AB = 30 см. Знайти периметр трикутника DBF.

• Дотичною до кола називається пряма, що має з колом одну спільну точку.
• Відрізки дотичних до кола, проведених з однієї точки, рівні.

Розв'язання

За умовою АВ=30 см.

За властивістю дотичних, проведених з однієї точки ВС=ВА=30 см.

За аксиомою вимірювання відрізків:

АВ=AD+DB, но AD=DE (за властивістю дотичних), тому AB=DE+DB.

BC=CF+FB, но CF=EF (за властивістю дотичних), тому BC=EF+FB.

Периметр трикутника дорівнює сумі всіх його сторін:

=AB + BC = 30 + 30 = 60 (см)

Відповідь: Р(DBF) =60 см

#SPJ1