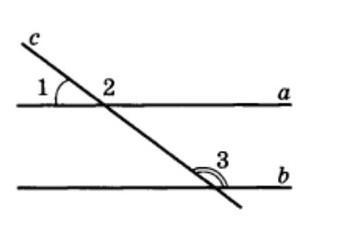
на рисунке угол 1=37°, угол 3=143°. Докажите, что a||b, и найдите угол 2
Ответы на вопрос
Ответ:
∠2=143°
Объяснение:
∠2=180°-37°=143° (по свойству смежных углов)
∠2 и ∠3 - соответственные. Если соответственные углы равны, то прямые параллельны (по признаку) ⇒ a║b.
Подобным образом можно доказать параллельность через ∠1.
ИЛИ
∠2=180°-37°=143° (по свойству смежных углов)
Угол, вертикальный углу 2 тоже равен 143° (по свойству вертикальных углов). Обозначим этот угол цифрой 4.
Тогда получили, что ∠3=∠4. Эти углы - внутренние накрест лежащие. Если внутренние накрест лежащие углы равны, то прямые параллельны (по признаку) ⇒ a║b.
Подобным образом можно доказать параллельность через ∠1.
Ответ: =============================================================
если <1+<2=180* то они смежные, <3||<2 поскольку прямые
"a" и "b" пересекает одна и таже секущая "c" отсюда следует что
<1+<2=180*
1) 37+143=180( примая "a" ровная)
2)чтобы найти углы "b" надо
180*-<3=<1 =>
=> "a" || "b"