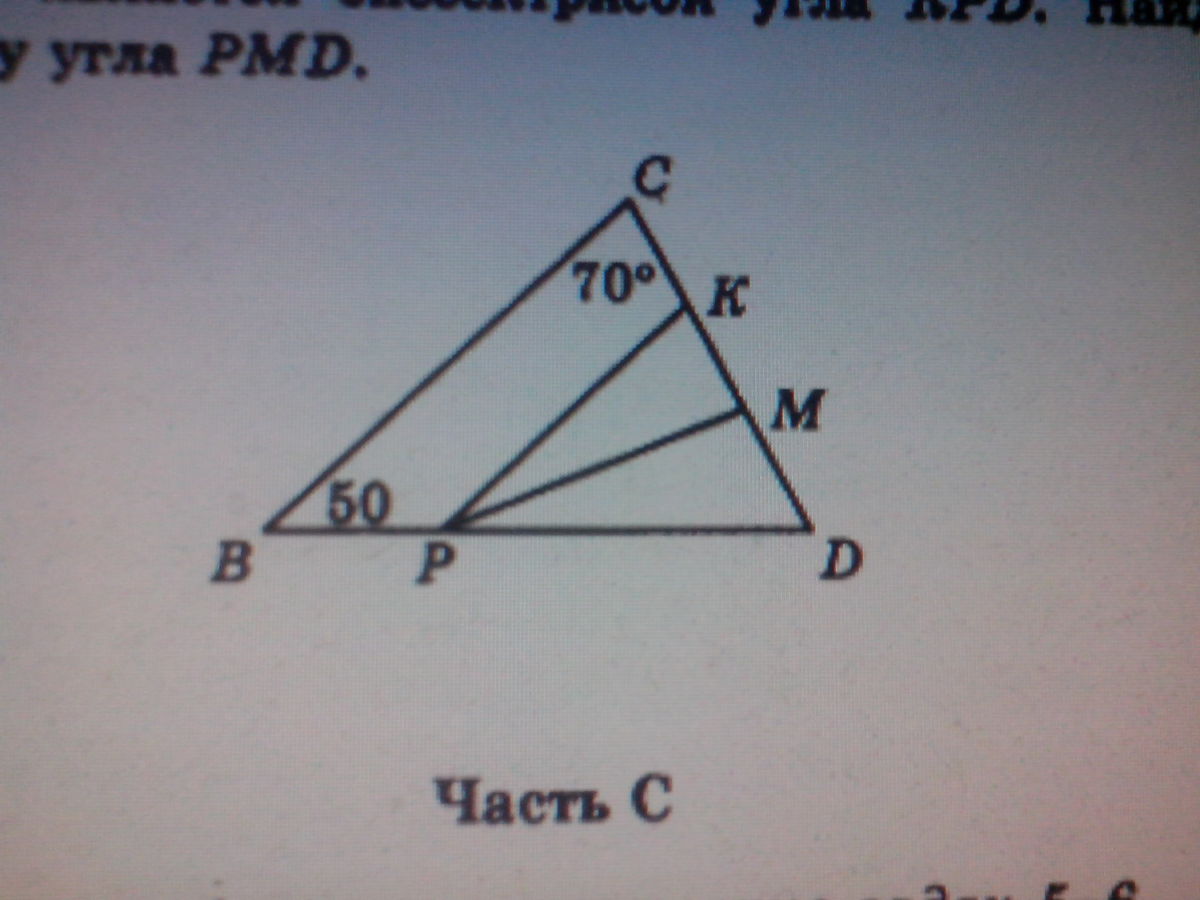
На рисунке отрезок PK параллелен стороне BC, луч PM является биссектриссой угла KPD.Найдите величину угла PMD
Приложения:
Ответы на вопрос
Ответил KuOV
0
Сумма углов треугольника равна 180°.
∠CDB = 180° - (50° + 70°) = 180° - 120° = 60°
∠KPD = ∠CBD = 50° как соответственные при пересечении КР║СВ секущей BD.
∠MPD = 1/2 ∠KPD = 25°, так как РМ - биссектриса ∠KPD.
Из ΔMPD:
∠PMD = 180° - (∠MPD + ∠MDP) = 180° - (25° + 60°) = 180° - 85° = 95°
∠CDB = 180° - (50° + 70°) = 180° - 120° = 60°
∠KPD = ∠CBD = 50° как соответственные при пересечении КР║СВ секущей BD.
∠MPD = 1/2 ∠KPD = 25°, так как РМ - биссектриса ∠KPD.
Из ΔMPD:
∠PMD = 180° - (∠MPD + ∠MDP) = 180° - (25° + 60°) = 180° - 85° = 95°
Новые вопросы