На рисунке ниже дaн треугольник ABC и прямая k: Укажи вершины треугольника, симметричного треугольнику ABC относительно прямой k: у 6 Ks BILIM Land B 5 4 3 НА C 1 І 1 2 3 8 7 6 5 4 3 4 -2 -1 0 -1 -2 -3 -4 -5 -6 Ответ. А,( 0 : 2 ), B, C, , C, D, ). PYC​

Ответ:

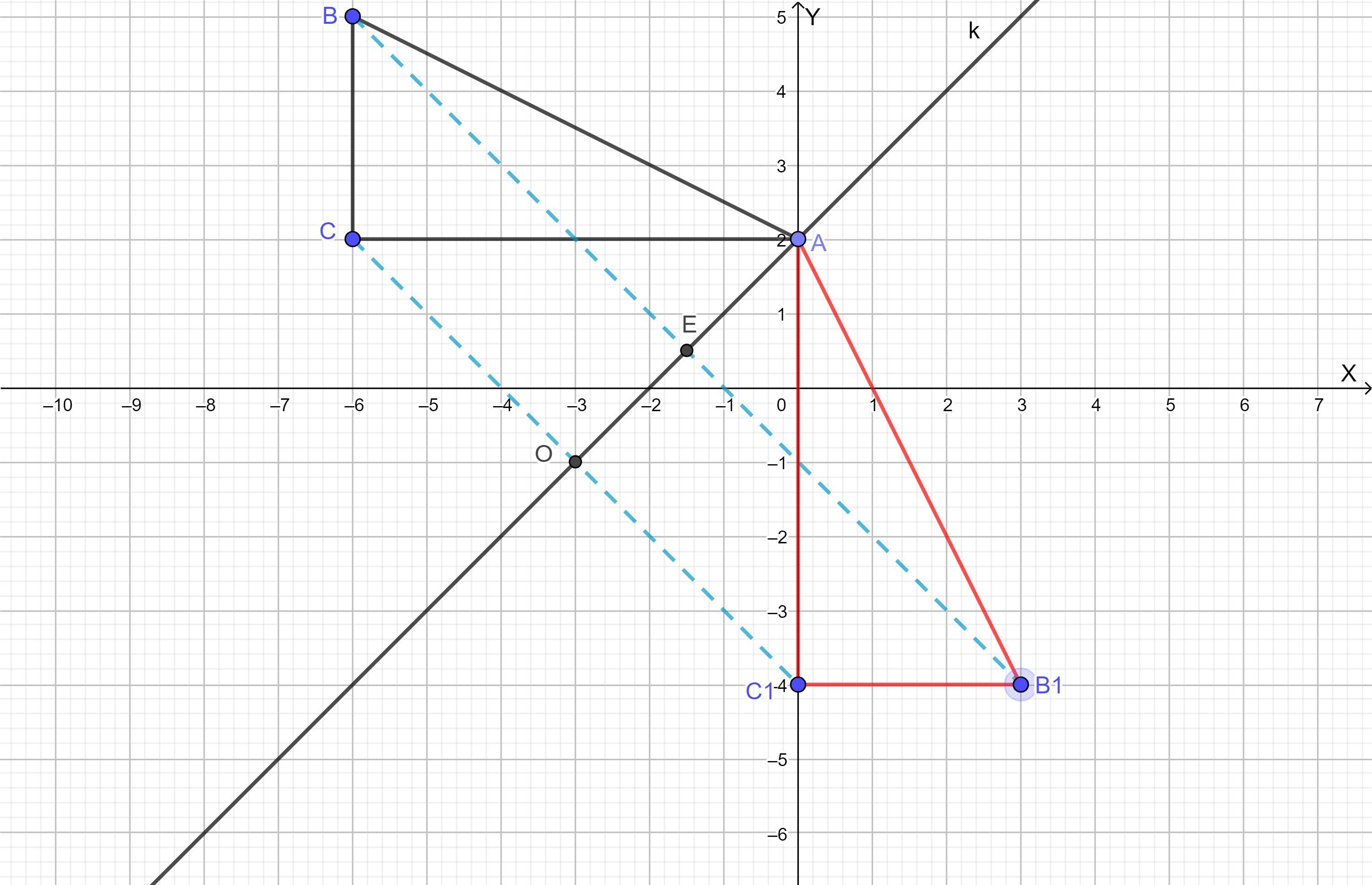
Мы получили треугольник АВ1С1 симметричный треугольника АВС относительно прямой k с вершинами :А( 0; 2) ; В1 ( 3; -4) ; С1 ( 0; -4) , рисунок во вложении.

Пошаговое объяснение:

Указать вершины треугольника, симметричного треугольнику ABC относительно прямой k.

Осевая симметрия — это симметрия относительно прямой.

Чтобы построить треугольник, симметричный треугольнику АВС относительно прямой k, достаточно построить точки, симметричные вершинам треугольника, и соединить их отрезками.

Чтобы построить точку, симметричную некоторой точке A относительно прямой g, надо:

1) Провести из точки A к прямой g перпендикуляр AO.

2) На продолжении перпендикуляра с другой стороны от прямой g отложить отрезок OA1, равный отрезку AO: OA1=AO.

Полученная точка A1 симметрична точке A относительно прямой g.

Как видим, надо построить две точки симметричные относительно прямой k - это т.В1 и С1, поскольку вершина А ( 0; 2) будет общая для обоих треугольников.

Проведем перпендикуляр из СО к прямой k.

На продолжении перпендикуляра по другую сторону прямой k отложим отрезок равный отрезку СО (рисунок во вложении) и поставим точку С1 (0; -4).

Теперь проведем перпендикуляр ВЕ к прямой k.

На продолжении перпендикуляра по другую сторону прямой k отложим отрезок равный отрезку ВЕ (рисунок во вложении) и поставим точку В1 (3; -4).

Теперь соединим т.С1 и т.В1 , затем т. В1 и т.А , а также т.С1 и т.А.

Мы получили треугольник АВ1С1 симметричный треугольника АВС относительно прямой k с вершинами :

А( 0; 2) ; В1 ( 3; -4) ; С1 ( 0; -4)