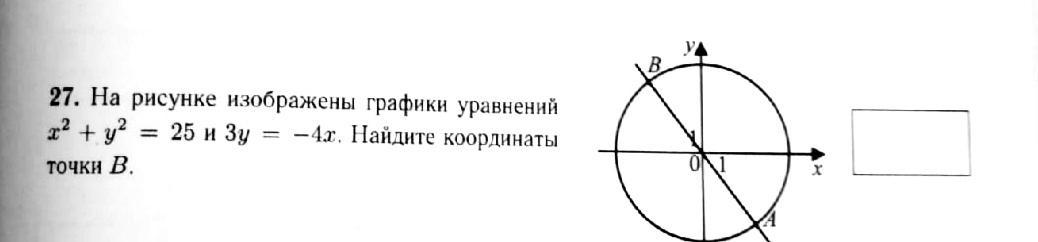
Алгебра, вопрос задал albinaanikanova , 2 года назад

На рисунке изображены графики уравнений x^2+y^2=25 3y=-4x Найдите координаты точки B

Приложения:

Ответы на вопрос

Ответил lilyatomach

Ответ:

В ( -3; 4) .

Объяснение:

Чтобы найти координаты точки пересечения графиков, надо решить систему уравнений.

$\left \{\begin{array}{l} x^{2} +y^{2} = 25, \\ 3y = -4x; \end{array} \right.\Leftrightarrow \left \{\begin{array}{l} x^{2} +\left(-\dfrac{4}{3}x\right) ^{2} = 25, \\ y = -\dfrac{4}{3} x; \end{array} \right.\Leftrightarrow\left \{\begin{array}{l} x^{2} +\dfrac{16}{9}x^{2} = 25|\cdot9, \\\\ y = -\dfrac{4}{3} x; \end{array} \right.\Leftrightarrow$

$\Leftrightarrow \left \{\begin{array}{l} 9x^{2} +16x^{2} = 25\cdot9, \\ y = -\dfrac{4}{3} x; \end{array} \right.\Leftrightarrow\left \{\begin{array}{l} 25x^{2} = 25\cdot9, \\ y = -\dfrac{4}{3} x; \end{array} \right.\Leftrightarrow\left \{\begin{array}{l} x^{2} = 9, \\ y = -\dfrac{4}{3} x; \end{array} \right.\Leftrightarrow$

$\left \{\begin{array}{l} \left [\begin{array}{l} x = -3, \\ x = 3 \end{array} \right., \\ y = -\dfrac{4}{3} x; \end{array} \right.\Leftrightarrow \left [\begin{array}{l} \left \{\begin{array}{l} x = 3, \\ y =- 4; \end{array} \right. \\ \left \{\begin{array}{l} x= -3, \\ y = 4. \end{array} \right. \end{array} \right.$

Тогда (3; -4) и (-3; 4) - точки пересечения графиков.

Точка В находится во второй четверти. Значит, В ( -3; 4) .

Предыдущий вопрос

Следующий вопрос

Новые вопросы

Другие предметы, 1 год назад

какие государства существовали в 5 по 9 века на территории поводжья?)...

Английский язык, 1 год назад

Colin 's grandmother is seventy-four. Her mane is Ann White. She lives in Bath which is a small town in the United Kingdom. She loves her grandchildren. They are students in Bath. She looks after her...

Алгебра, 2 года назад

график обратной пропорциональности проходит через точки А (-8; 7) и В (х; -14). найдите значение х...

Алгебра, 2 года назад

Решите, очень нужно...

Биология, 7 лет назад

Умоляю помогите!!! Биология!!! Номер 9!И если можете просто проверьте номер 8 если видно и скажите верно или нет?

Химия, 7 лет назад

Массы соли и воды относятся как 1:8.Определите массовую долю соли в растворк...