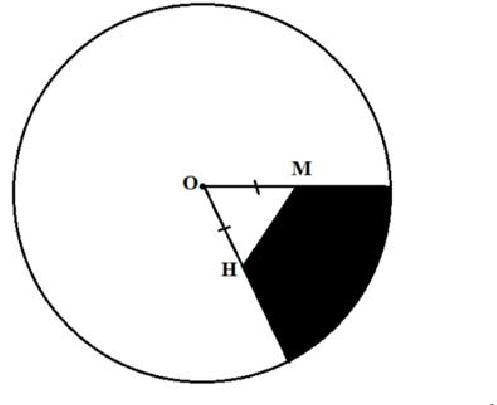
На рисунке изображен сектор круга с центром в точке О и радиусом,
равным 18 см. ОМ =ОН= 8 см, и = 60°. Найдите площадь закрашенной
области.
Даю 100 баллов срочно!!!!!!!!!!

Ответ:

Объяснение:

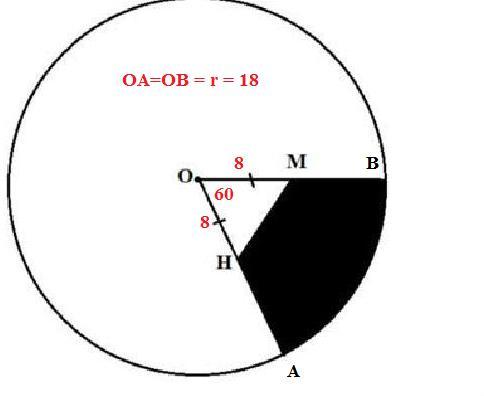
Никаких специальных формул применять не будем. Так как центральный угол АОВ= 60 градусов, то сектор АОВ составляет 60/360 = 1/6 часть площади круга.

Площадь круга S=

Тогда площадь сектора в 6 раз меньше и составляет

кв см

Теперь осталось вычесть из  площади сектора площадь треугольника НОМ. Найдем ее.

кв см

Тогда площадь заштрихованной части

кв см