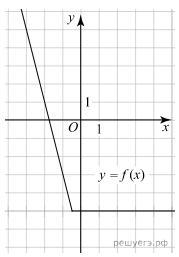
На рисунке изображён график функции вида f(x)=ax+| bx + c | + d, где числа a, b, c и d — целые. Найдите корень уравнения ax + d=0.
(bx+c в модуле)
Приложения:
dnepr1:
a=-2, b=-2, c=-1, d=-6.
Ответы на вопрос
Ответил Удачник66
10
Ответ:
x = -3
Объяснение:
По графику видно, что прямые пересекаются в точке (-0,5; -5).
Значит, под модулем стоит |2x+1|, и при x = -0,5 он обращается в 0.
Левая прямая проходит через точки (-1; -3) и (-2; 1).
Ее уравнение:
(x+1)/(-2+1) = (y+3)/(1+3)
(x+1)/(-1) = (y+3)/4
4(x+1) = -(y+3)
4x + 4 = - y - 3
y = -4x - 7
Правая прямая: y = -5
Значит, при x < -0,5 будет:
y = ax + (-2x-1) + d = -4x - 7
(a-2)x + (d-1) = -4x -7 (1)
А при x ≥ -0,5 будет:
y = ax + (2x+1) + d = -5
(a+2)x + (d+1) = -5 (2)
Из этих двух уравнений получаем:
a = -2; d = -6.
Итак, получили: a = -2; b = 2; c = 1; d = -6.
Уравнение ax + d = 0 выглядит так:
-2x - 6 = 0
Его корень: x = -3
Новые вопросы
Математика,
1 год назад
Другие предметы,
1 год назад
Другие предметы,
6 лет назад
Алгебра,
6 лет назад
Литература,
8 лет назад