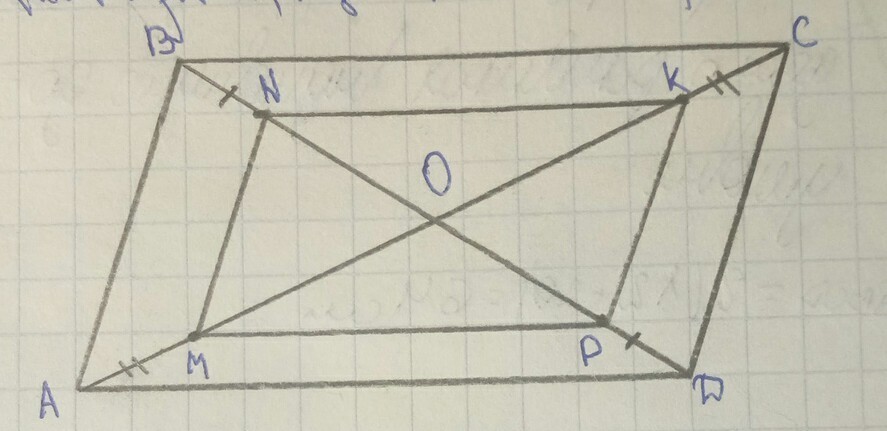
На рисунке ABCD параллелограмм, AM=KC, BN=PD. Докажите, что MP=NK, MN||PK
Приложения:
Ответы на вопрос
Ответил Hrisula
0
ABCD параллелограмм, AM=KC, BN=PD
Диагонали параллелограмма пересекаются и точкой пересечения делятся пополам.
МО=АО -АМ, ОК=СО - КС. По условию АМ=СК, следовательно, МО=ОК.
Аналогично доказывается равенство NO=ОР.
МО=ОK, NO=OД. Диагонали четырехугольника МNKP пересекаются и точкой пересечения делятся пополам. Из признаков параллелограмма:
Если диагонали четырехугольника пересекаются и в точке пересечения делятся пополам, то этот четырехугольник ― параллелограмм. ⇒ МNKP- параллелограмм.
В параллелограмма противоположные стороны равны и параллельны. Следовательно, MP=NK, MN||PK, что и требовалось доказать.
Новые вопросы