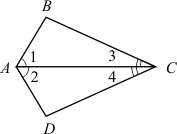
На рисунке AB = AD, BC = CD. Докажите, что луч АС – биссектриса угла BAD.
Приложения:
Ответы на вопрос
Ответил chimita02
0
с начало мы должны доказать что ΔАВС=ΔАDC:
Рассмотрим ΔАВС и ΔАDC по условию AB=AD,BC=CD.AC- общая сторона треугольников.⇒ΔАВС=ΔАDC по третьему признаку равенства треугольников.⇒Если ΔАВС=ΔАDC то и углы тоже равны⇒угол BAC=углу DAC.Мы знаем что биссектриса делит угол пополам т.е. разделенные углы равны⇒ AC-биссектриса угла BAD ч.т.д.
Рассмотрим ΔАВС и ΔАDC по условию AB=AD,BC=CD.AC- общая сторона треугольников.⇒ΔАВС=ΔАDC по третьему признаку равенства треугольников.⇒Если ΔАВС=ΔАDC то и углы тоже равны⇒угол BAC=углу DAC.Мы знаем что биссектриса делит угол пополам т.е. разделенные углы равны⇒ AC-биссектриса угла BAD ч.т.д.
Ответил alanbaskaev2015
0
что значит чтд?
Ответил chimita02
0
что и требовалось доказать)
Новые вопросы