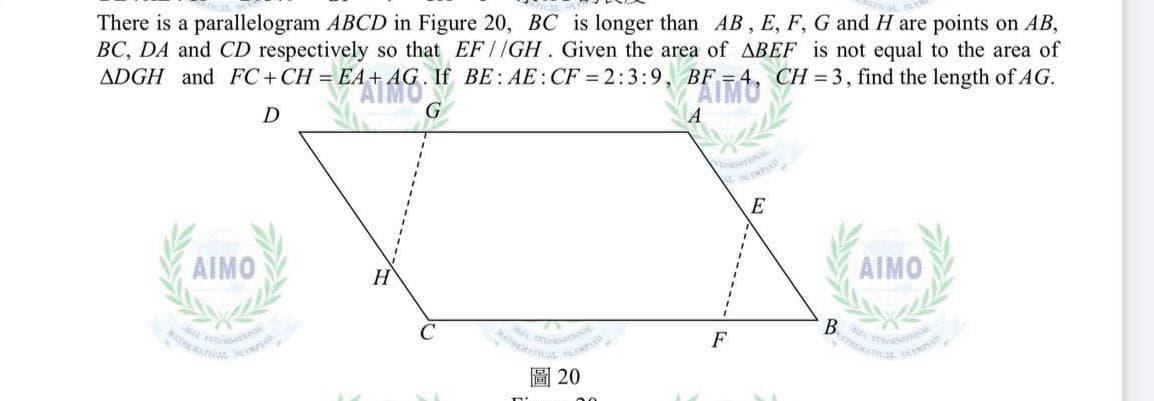
На рисунке 20 . Параллелограмм ABCD ; в котором BC длиннее AB ; точки Е , F , G и H точки находятся на сторонах AB , BC , DA и CD соотвественно ; так что EF // GH . Если Площадь ΔBEF не равна площади Δ DGH ; и FC+CH=EA+AG . А также BE:AE: CF=2:3:9 ; BF=4 , CH=3 . Найдите длину AG =?

Ответ:

15 ....................................

Объяснение:

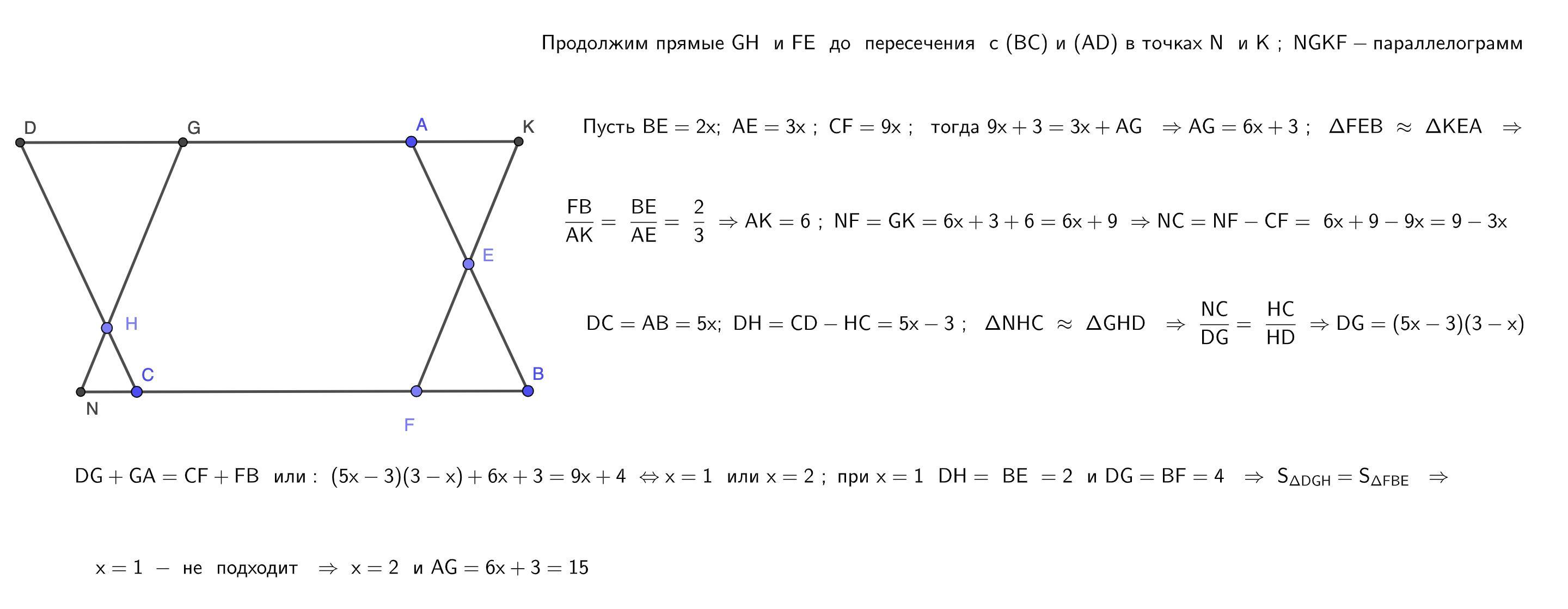
Докажем, что из условия FC+CH=EA+AG следует, что △EBF - равнобедренный.

Рассмотрим равные треугольники E1BF1 и HDG (E1F1||GH). Условие очевидно выполняется (F1C=AG, E1A=CH).

Теперь рассмотрим данный отрезок EF. Если условие выполняется, то EE1=FF1. Тогда EE1F1F - равнобедренная трапеция, углы при основании равны. Следовательно △EBF также равнобедренный.

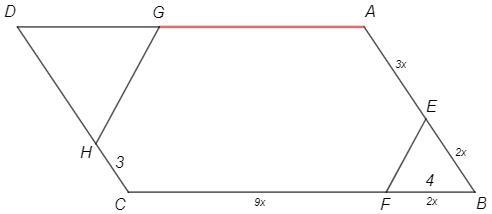
BE=BF=2x, AE=3x, CF=9x

BF=2x=4 => x=2

FC+CH=EA+AG => 9x+3 =3x+AG => AG =18+3-6 =15