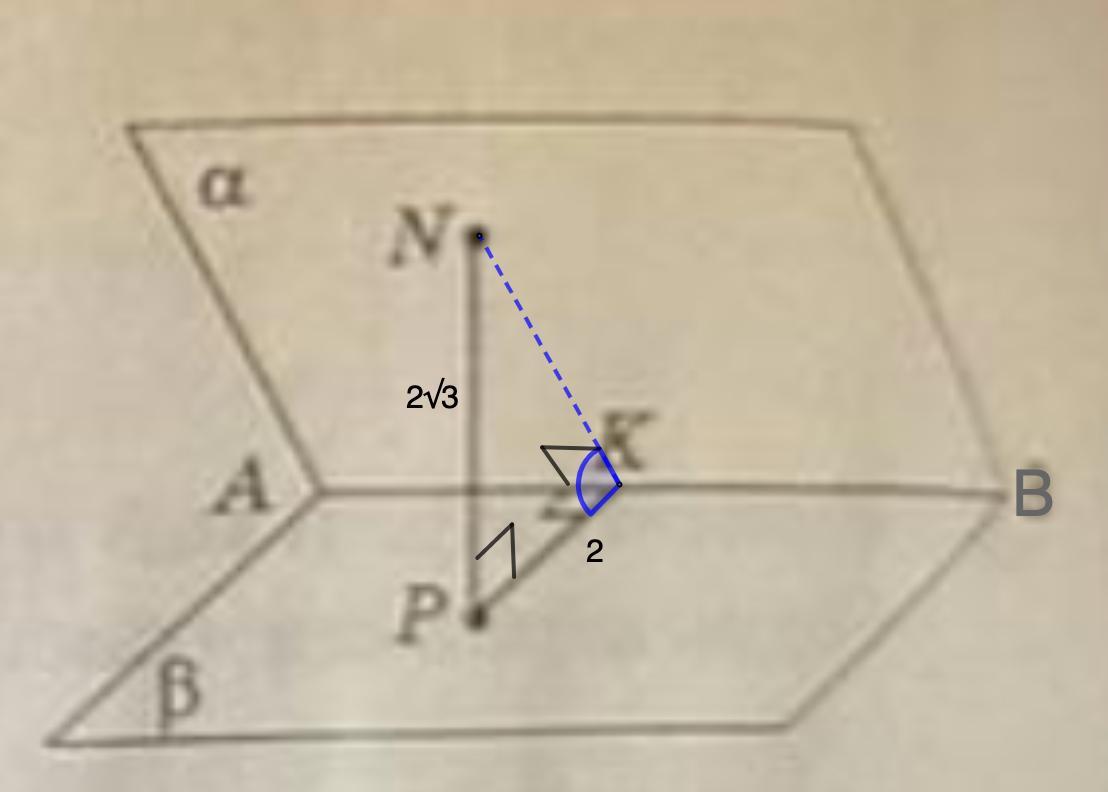
На рис. 3 зображено двогранний кут з ребром АВ. Знайдіть градусну міру цього кута, якщо
PК|AB, РК = 2, точка N належить площині a , NP | B, NP - 2/3 .
Ответы на вопрос
Ответ:
Градусная мера данного двугранного угла равна 60°.
Объяснение:
На рис. 3 изображен двугранный угол с ребром АВ. Найдите градусную меру этого угла, если PK ⊥ AB, PК =2, точка N принадлежит плоскости α, NP ⊥ β, NP=2√3.
Дано: NABP - двугранный угол;
PK ⊥ AB, PК =2;
N ∈ α;
NP ⊥ β, NP=2√3
Найти: градусную меру угла NABP.
Решение:
Двугранный угол измеряется своим линейным углом.
- Линейный угол образован пересечением двугранного угла с плоскостью, перпендикулярной к его ребру.
То есть, если взять точку на ребре двугранного угла, провести лучи в каждой плоскости перпендикулярные этому ребру, то эти перпендикуляры и будут сторонами линейного угла.
Определим искомый угол.
Соединим точки К и N.
РК ⊥ АВ (условие)
NP ⊥ β ⇒ PK - проекция NK на β.
- Прямая, проведенная на плоскости через основание наклонной перпендикулярно ее проекции, перпендикулярна и самой наклонной.
⇒ NK ⊥ AB
⇒ ∠NKP - искомый линейный угол двугранного угла.
Рассмотрим ΔPNK.
- Если прямая перпендикулярна плоскости, то перпендикулярна любой прямой, лежащей в этой плоскости.
⇒ NP ⊥ PK ⇒ ΔPNK - прямоугольный.
- Тангенс угла - отношение противолежащего катета к прилежащему.
⇒ ∠NKP = arctg √3 = 60°
Градусная мера данного двугранного угла равна 60°.