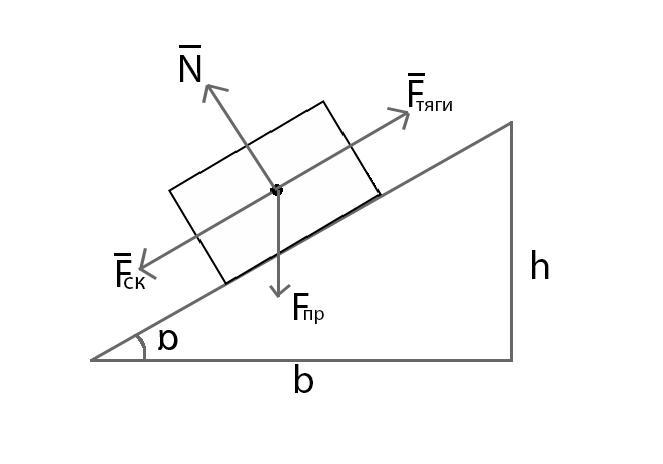
На похилу площину довжиною 5 м , висотою 3 м покладено вантаж масою 75
кг. Обчислити величину сили, що тягне тіло вздовж похилої площини вгору , якщо при коефіцієнті тертя 0,2 тіло має прискорення руху 2 м/с2.

Відповідь:

Сила тяги, що діє на тіло, дорівнює 350 Н.

Пояснення:

Дано:

b = 5 м
h = 3 м
m = 75 кг
μ = 0,2
α = 2 м/с²
g = 9,8 м/с² ≈ 10 м/с²

Знайти: F(тяги)

Розв'язок:

За другим законом Ньютона:

F(тяги) + F(оп) + N + mg = ma

Спроектуємо рівняння на осях координат:

{OX: F(тяги) - F(оп) - mgsin(α) = -ma,
{OY: N - mgsin(α) = 0

Розв'яжемо отриману систему, урахувавши, що F(оп) = μmgcos(α):

{ F(тяги) = F(оп) + mgsin(α) - ma,
{ F(оп) = μmgcos(α)

F(тяги) = μmgcos(α) + mgsin(α) - ma = m(μgcos(α) + gsin(α) - a)

За теоремою Піфагора знайдемо с (гіпотенузу прямокутного трикутника):

c² = h² + b²
c = √(h² + b²)
c = √(3² + 5²) = √36 = 6 (м)

За тригонометричними формулами знайдемо cos і sin кута альфа:

{ cos(α) = b / c = ,

{ sin(α) = h / c = 3 / 6 = 0,5.

Обчислимо силу тяги:

F(тяги) = 75 кг * (0,2 * 10 м/с² * (5/6) + 10 м/с² * 0,5 - 2 м/с²) = 350 H

Відповідь: F(тяги) = 350 Н.

#SPJ1