На отрезке AB выбрана точка C так что AC=72 и BC=3. Построена окружность с центром A, проходящая через C. Найдите длину отрезка касательной, проведённой из точки B к этой окружности.

Ответ:

21 (единиц)

Пошаговое объяснение:

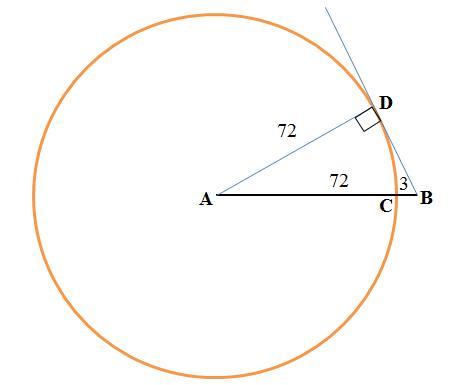
Дано (см. рисунок):

AC=72

BC=3

A - центр окружности

R = AC = 72 - радиус окружности

Найти: BD - отрезок касательной.

Решение.

Касательная к окружности перпендикулярна радиусу окружности. В силу этого треугольник ΔADB прямоугольный с ∠D=90°.

В треугольнике ΔADB катет AD=72, а гипотенуза AB=AC+CB=72+3=75.

По теореме Пифагора

AB²=AD²+BD² или BD² = AB² - AD².

По известным данным находим BD:

BD² = AB² - AD²=75²-72²=(75-72)·(75+72)=3·147=441=21²

или BD = 21 (единиц).