На меньшей дуге AC описанной окружности остроугольного треугольника ABC выбрана точка D . На стороне AC нашлась такая точка E , что DE=AE . На прямой, параллельной AB , проходящей через точку E , отмечена точка F , причём CF=BF . Докажите, что точки D , E , C и F лежат на одной окружности

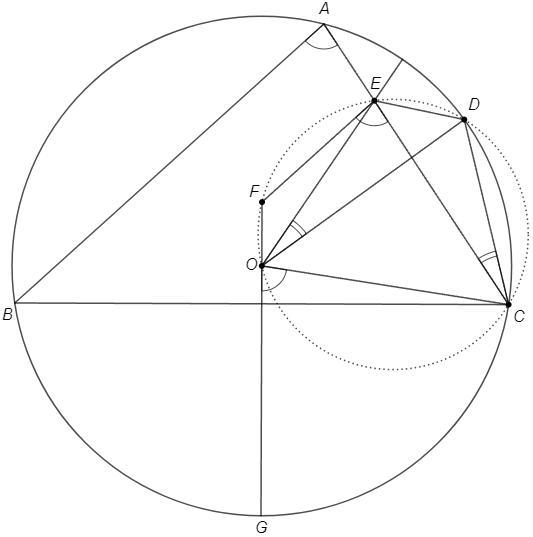
O - центр описанной окружности △ABC, точка пересечения серединных перпендикуляров.

OE, OG - серединные перпендикуляры.

∠COG =◡BC/2 (серединный перпендикуляр делит дугу пополам) =∠BAC

∠BAC=∠FEC (соответственные при AB||EF)

=> ∠COG=∠FEC

=> OFEC - вписанный четырехугольник (внешний угол равен противолежащему внутреннему)

∠EOD =◡AD/2 =∠ACD

=> OEDC - вписанный четырехугольник (отрезок ED виден из точек O и C под равным углом)

=> точки FEDC лежат на одной окружности.