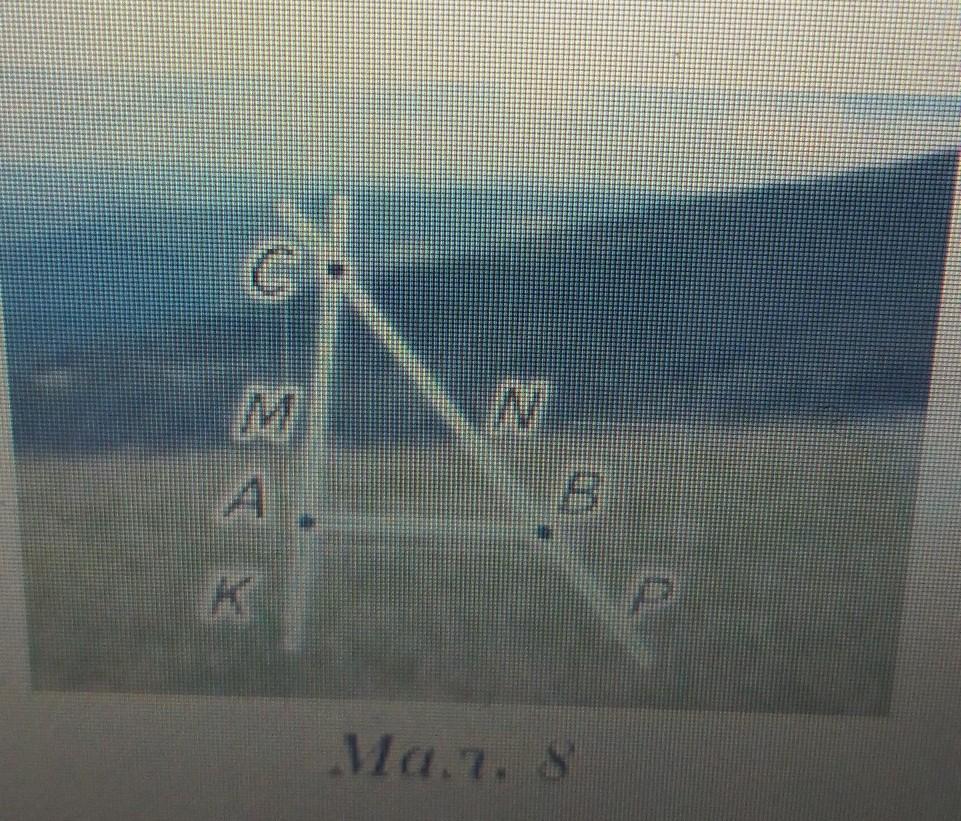
На Мал. 8 зображено дві прямі дороги KM і PN, що перетинаються десь за лісом у недоступній точці С. Потрібно знайти відстань від деякого пункту А на дорозі КМ до точки С перетину доріг. Для цього позначили на дорозі PN пункт В так, щоб можна було виміряти відстань AB, і визначили кути ВАМ і ABN. Поясніть спосiб знаходження відстані АС. Обчисліть АС, якщо АВ = 800 м. /ВАМ = 85º, ZABN = 52º.
Ответы на вопрос
Ответ:
Для знаходження відстані АС можна скористатися теоремою про перетин двох прямих, яка стверджує, що сума кутів, утворених перетином двох прямих, дорівнює 180 градусам. Оскільки ми знаємо кути ВАМ і ABN, можемо знайти кут МВН, використовуючи властивість, що сума кутів в трикутнику дорівнює 180 градусам:
МВН = 180 градусів - ВАМ - ABN = 180 градусів - 85 градусів - 52 градуси = 43 градуси.
Далі, можна використати трикутник АВС, що містить кути АВС, САВ та СВА. Оскільки САВ дорівнює 90 градусам, можемо знайти кут АВС, використовуючи властивість, що сума кутів в трикутнику дорівнює 180 градусам:
АВС = 180 градусів - АВН - НВС = 180 градусів - (180 градусів - МВН) - (180 градусів - ABN) = МВН - ABN = 43 градуси - 52 градуси = -9 градусів.
Оскільки кут АВС від'ємний, це означає, що точка С знаходиться з іншого боку від А на дорозі КМ. Тому, щоб знайти відстань АС, ми повинні продовжити дорогу КМ в напрямку, протилежному до точки В, до тих пір, поки не знайдемо точку С. Оскільки ми знаємо кути ВАМ і МВН, можемо використати тригонометричні функції, щоб знайти відстань АС. Але оскільки ми не знаємо відстані між точками В і С, ми не можемо безпосередньо застосувати тригонометричні функції для знаходження відстані АС.
Объяснение:
Ответ:Для знаходження відстані АС можна скористатися теоремою синусів для трикутника АВС:
sin(ВАМ) = AC / AB => AC = AB * sin(ВАМ)
Аналогічно, застосовуючи теорему синусів для трикутника АВN, можна знайти довжину BN:
sin(ABN) = BN / AB => BN = AB * sin(ABN)
Оскільки точка С знаходиться на перетині доріг КМ і PN, то трикутники АСК і СВС є подібними за кутовою мірою. Тому використовуючи співвідношення між сторонами подібних трикутників, можна записати:
AC / BN = AS / BS
де AS - відстань від точки А до точки перетину доріг, а BS - відстань від точки В до точки перетину доріг.
Оскільки точка В відома, можна виразити BS через відстань AB і відстань BM, яку можна знайти, використовуючи теорему косинусів для трикутника ВАМ:
cos(ВАМ) = BM / AB => BM = AB * cos(ВАМ)
Підставляючи ці значення, отримуємо:
AC / (AB * sin(ABN)) = AS / (AB - AB * cos(ВАМ))
Або ж:
AC = AS * sin(ABN) * (AB - AB * cos(ВАМ)) / AB
Тепер застосуємо теорему синусів до трикутника АВМ, щоб знайти відстань AS:
sin(АВМ) = AS / AB => AS = AB * sin(АВМ)
Для знаходження кута АВМ можна скористатися властивістю кутів на протилежних вершинах паралельних прямих:
АВМ + ZABN = 180º => АВМ = 180º - ZABN
Підставляючи ці значення, ми отримуємо:
AC = AB * sin(180º - ZABN) * (1 - cos(ВАМ))
= AB * sin(ZABN) * (1 - cos(ВАМ))
Підставляючи дані, отримуємо:
AC = 800 м * sin(52º) * (1 - cos(85º))
≈ 1464 м
Таким чином, відстань від точки А до точки перетину д
Объяснение:.