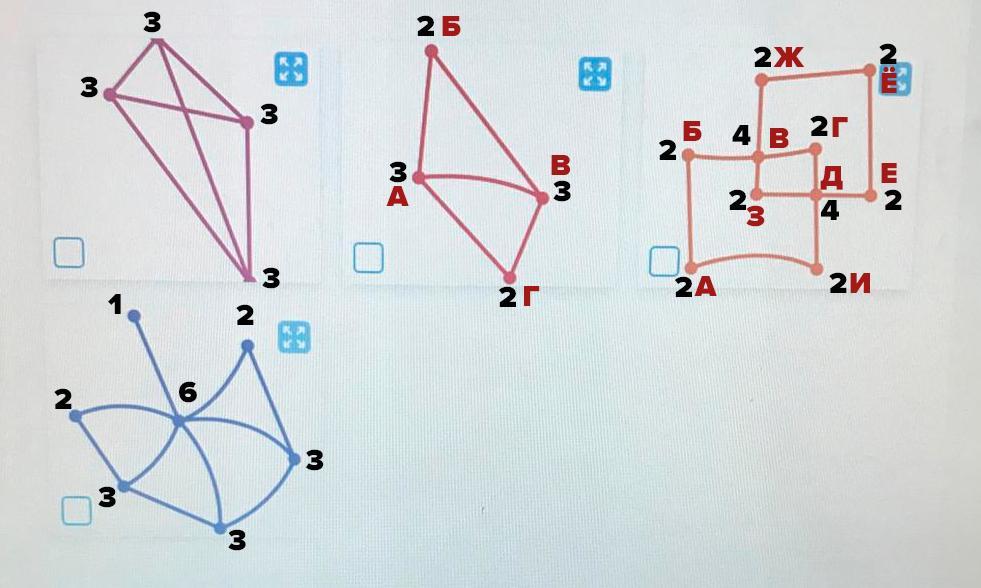
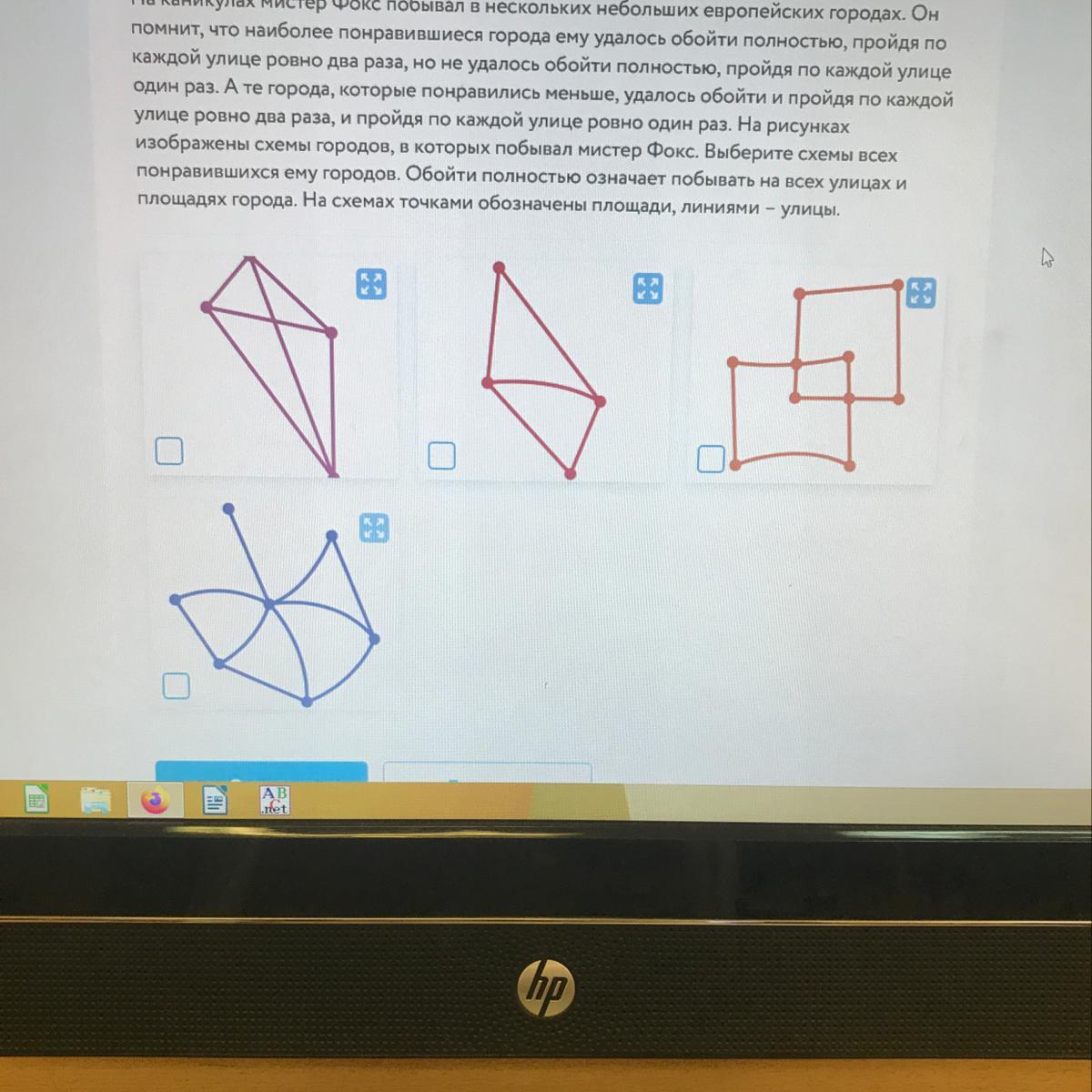
На каникулах мистер Фокс побывал в нескольких небольших европейских городах. Он помнит, что наиболее понравившиеся города ему удалось обойти полностью, пройдя по каждой улице ровно два раза, но не удалось обойти полностью, пройдя по каждой улице один раз. А те города, которые понравились меньше, удалось обойти и пройдя по каждой улице ровно один раз, и пройдя по улице ровно два раза. На рисунках изображены схемы городов, в которых побывал Мистер Фокс. Выберите схемы всех понравившийся ему городов. Обойти полностью означает побывать на всех улицах и площадях города. На схемах точками обозначены площади, линиями - улицы.
Ответы на вопрос
Ответ:
1, 4
Объяснение:
Рассмотрим путь по такому городу, который проходит по каждой улице не более чем по одному разу.
Простое наблюдение: если какая-то площадь не является началом или концом пути, то из неё должно вести чётное число дорог: по одной дороге в город нужно войти, из другой выйти, и так каждый раз.
Значит, в если в городе есть больше двух городов, из которых ведут нечетное число дорог, то его нельзя обойти, пройдя по каждой улице один раз, так что они точно понравились мистеру Фоксу.
На рисунке черным цветом указано число дорог для каждой площади. Получается, что города 1 и 4 мистеру Фоксу понравились. В городах 2 и 3 можно предложить маршрут, который проходит по каждой улице по одному разу: для 2 это, например, АБВАГВ, для 3 АБВГДЕЁЖВЗДИА - так что эти города понравились мистеру Фоксу не так сильно.