Алгебра, вопрос задал el0os , 1 год назад

на какую цифру заканчивается число 8^99

Ответы на вопрос

Ответил igundane

$8^{4*24}$ оканчивается на тоже число ,что и $8^4$

Приложения:

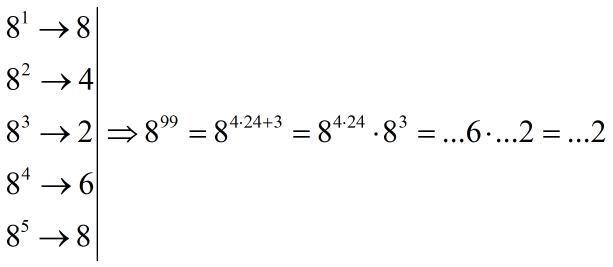
Нау4пок: здравствуйте! я очень извиняюсь, но вряд ли будет правильно, если вы будете писать 8^1=8, 8^2=4.. Не мог ли бы вы исправить?

Нау4пок: конечно подскажу! только вопрос в том, что будет ли это для школьного уровня... стучите в ЛС, если хотите)

Нау4пок: да, вроде проходят, но делению не уделяют особого внимания, да и вряд ли все люди знают смысл операции mod

Нау4пок: если хотите через div/mod то можно, но желательно объяснить, что первое целая часть от деления, а второе остаток. Дать пример, типа: 10 mod 3 = 1, а 10 div 3 = 3. также стоит ввести понятие тождественно равных выражений(те выражения, которые ...) привести пару примеров (желательно сразу ввести понятие)

Нау4пок: всегда рад!

Ответил Нау4пок

Для начала попробуем отследить закономерность в степенях 8:

${8}^{1} = 8 \\ 8^{2} = 64 \\ {8}^{3} = 512 \\ {8}^{4} = 4096 \\ 8 ^{5} = 32768$

Каждое предыдущее число в конце отличается на 4(т.е. буквально имеем цикл, закономерность чисел, стоящих в конце): 8-4-2-6(на пятом члене цикла возвращается все обратно)

${8}^{99} = {8}^{24 \cdot 4 + 3}$

До того, как дойти до 99 степени, цикл совершается 24 раза, и ещё $\frac{3}{4}$ раза(т.е. совершается три элемента цикла из четырех). Как мы выяснили ранее, 3 элемент цикла кончается на двойку, а стало быть: