на фото.....................................................................
Приложения:
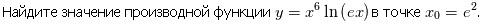
Ответы на вопрос
Ответил Аноним
0
Приложения:
Ответил Аноним
0
Так и думал, что (ln(ex))'=1/x
Ответил Матов
0
по правилу дифференцирования
![y=x^6*ln(ex)\
y'=x^6'ln(ex)+x^6*ln(ex)'=6x^5*ln(ex)+x^5=x^5(6ln(ex)+1)\
y'(e^2)=e^{10}*(6ln(e*e^2)+1)=e^{10}(6*3+1)=19*e^{10}](https://tex.z-dn.net/?f=y%3Dx%5E6%2Aln%28ex%29%5C%0Ay%27%3Dx%5E6%27ln%28ex%29%2Bx%5E6%2Aln%28ex%29%27%3D6x%5E5%2Aln%28ex%29%2Bx%5E5%3Dx%5E5%286ln%28ex%29%2B1%29%5C%0Ay%27%28e%5E2%29%3De%5E%7B10%7D%2A%286ln%28e%2Ae%5E2%29%2B1%29%3De%5E%7B10%7D%286%2A3%2B1%29%3D19%2Ae%5E%7B10%7D "y=x^6*ln(ex)\
y'=x^6'ln(ex)+x^6*ln(ex)'=6x^5*ln(ex)+x^5=x^5(6ln(ex)+1)\
y'(e^2)=e^{10}*(6ln(e*e^2)+1)=e^{10}(6*3+1)=19*e^{10}")
Приложения:
Новые вопросы