на фото 2 задания
50 баллов
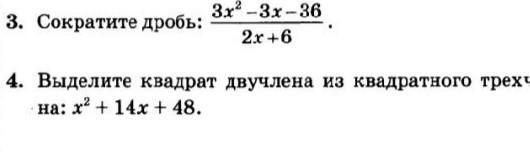
Ответы на вопрос
Ответ:
В решении.
Объяснение:
1) Сократить дробь:
(3х² - 3х - 36)/(2х + 6) =
= 3(х² - х - 12)/2(х + 3) =
в первых скобках выделить полный квадрат:
= 3((х² - 2*х*0,5 + 0,5²) - 0,5² - 12)/2(х + 3) =
в первых скобках получили квадрат разности; так как добавляли 0,5², нужно вычесть 0,5²:
= 3((х - 0,5)² - 0,25 - 12)/2(х + 3) =
= 3((х - 0,5)² - 12,25)/2(х + 3) =
в числителе разность квадратов, развернуть по формуле:
= 3(х - 0,5 - 3,5)*(х - 0,5 + 3,5)/2(х + 3) =
= 3(х - 4)(х + 3)/2(х + 3) =
(х + 3) и (х + 3) сократить на (х + 3):
= 3(х - 4)/2 = 1,5(х - 4).
2) Выделить полный квадрат:
х² + 14х + 48 =
= (х² + 2*х*7 + 7²) - 7² + 48 =
получили квадрат суммы, 7² добавляли, нужно вычесть:
= (х + 7)² - 49 + 48 =
= (х + 7)² - 1 =
получили разность квадратов, разложить по формуле:
= (х + 7 - 1)(х + 7 + 1) =
= (х + 6)(х + 8).