Алгебра, вопрос задал velikiiiy13 , 6 лет назад

можете помочь пожалуйста срочно!!!!

Приложения:

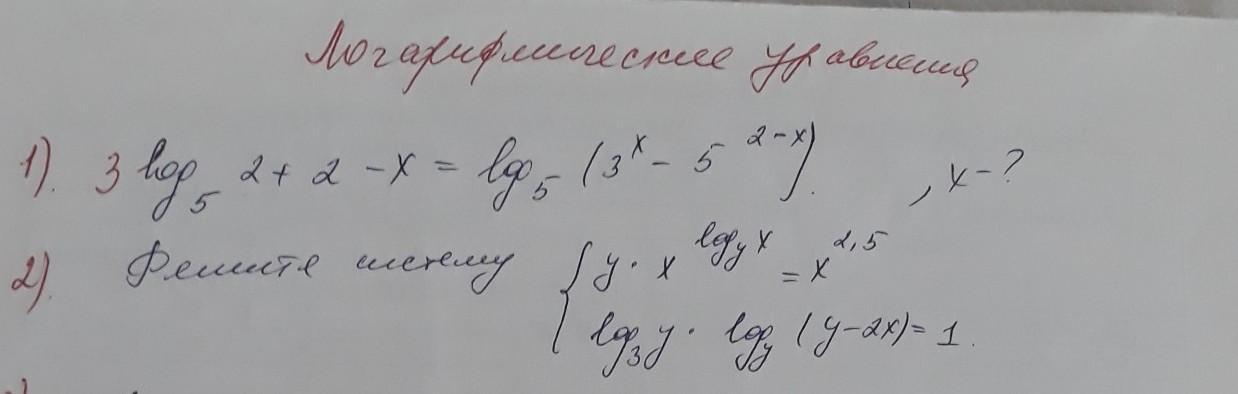
Simba2017: 1)х=2

Ответы на вопрос

Ответил sangers1959

2

Объяснение:

$1)\ 3*log_52+2-x=log_5(3^x-5^{2-x})\\log_52^3+log_55^2-log_55^x=log_5(3^x-5^{2-x})\\log_5\frac{8*25}{5^x}=log_5(3x-5^{2-x})\\ \frac{33}{5^x}=3^x-5^{2-x}\\ \frac{200}{5^x} =3^x-\frac{5^2}{5^x}\\3^x= \frac{200}{5^x}+\frac{25}{5^x} \\3^x=\frac{225}{5^x}\\ 3^x*5^3=225\\(3*5)^x=225\\15^x=15^2\\x=2.$

$2)\ \left \{ {{y*x^{log_yx}=x^{2,5}} \atop {log_3y*log_y(y-2x)=1}} \right. \\$

ОДЗ: х≥0 у≥0 у≠1 .

$y*x^{log_yx}=x^{2.5}.\\log_x(y*x^{log_yx})}=log_xx^{2,5}\\log_xy+log_xx^{log_yx}=2,5*log_xx\\log_xy+log_yx*log_xx=2,5\\log_xy+log_yx=2,5\\log_xy+\frac{1}{log_xy}=2,5\\ log^2_xy+1=2,5*log_xy\\log^2_xy-2,5log_xy+1=0.$

Пусть logₓy=t. ⇒

$t^2-2,5t+1=0\\D=2,25\ \ \ \ \ \\sqrt{D}=1,5\\ t_1=0,5\ \ \ \ t_2=2.\\t_1=log_xy=0,5\\y_1=x^{0,5}=\sqrt{x}. \\y_2=x^2.$

$log_3y*log_y(y-2x)=1\\log_y(y-2x)=\frac{1}{log_3y}=log_y3\\ y-2x=3\\y=2x-3.\\$

$1)\ \left \{ {{y=\sqrt{x} } \atop {y=2x+3}} \right. \ \ \ \ \Rightarrow\\\sqrt{x} =2x+3\\(\sqrt{x})^2=(2x+3)^2\\x=4x^2+12x+9\\4x^2+11x+9=0\\D=-23\ \ \ \ \Rightarrow\\x\in \varnothing.\\2)\ \left \{ {{y=x^2} \atop {y=2x+3}} \right. \ \ \ \ \ \Rightarrow\ \ \ \\x^2=2x+3\\x^2-2x-3=0\\D=16\ \ \ \ \sqrt{D}=4\\ x_1=-1\notin\\ x_2=3\in\ \ \ \ \ y=2*3+3=6+3=9.$

Ответ: (3;9).

Simba2017: а второе?

sangers1959: Я решаю дальше.

Simba2017: славно!

sangers1959: Всё.

velikiiiy13: спасибо огромное

Simba2017: в ответе разве не пара чисел?

sangers1959: Я уже исправил. Конечно, пара чисел.

imadrid: Используя тройной интеграл, вычислить объем тела 1) z²=4-x , x²+y²=4x

Simba2017: это наглость уже , по-моему!

Предыдущий вопрос

Следующий вопрос

Новые вопросы

Окружающий мир, 1 год назад

сообщение на тему монголо-татарское нашествие...

Русский язык, 1 год назад

#15!))))))))))))))))))))...

Математика, 6 лет назад

можете помочь пожалуйста как решается этот вопрос ...

Алгебра, 6 лет назад

Выполните задание пожалуйста) Упростите выражения: а) (3a − 2)^2 + (3a − 1)(2a + 1) − (3 − 11a) (15 баллов); б) 27y^2(x − y) − (x − 3y)^3 + x^3 (15 баллов). 20 балов даю...

Математика, 8 лет назад

1.Математичний диктант (для обох варіантів). - Запишіть вирази, знайдіть їх значення. 1)Частку чисел 8 і 1 збільшити на добуток чисел 10 і 0. 2)Різницю чисел 23 і 18 помножити на 1. 3)Добуток...

Алгебра, 8 лет назад

Геологи 4 ч летели на вертолёте со скоростью 80 км/ч, а затем ехали верхом 2 ч со скоростью 12 км/ч. Какой путь проделали геолаги за это время?