много болел, пришел на первый урок, а тут такое, можете пожалуйста решить, за флуд буду кидать жалобы

Ответ:

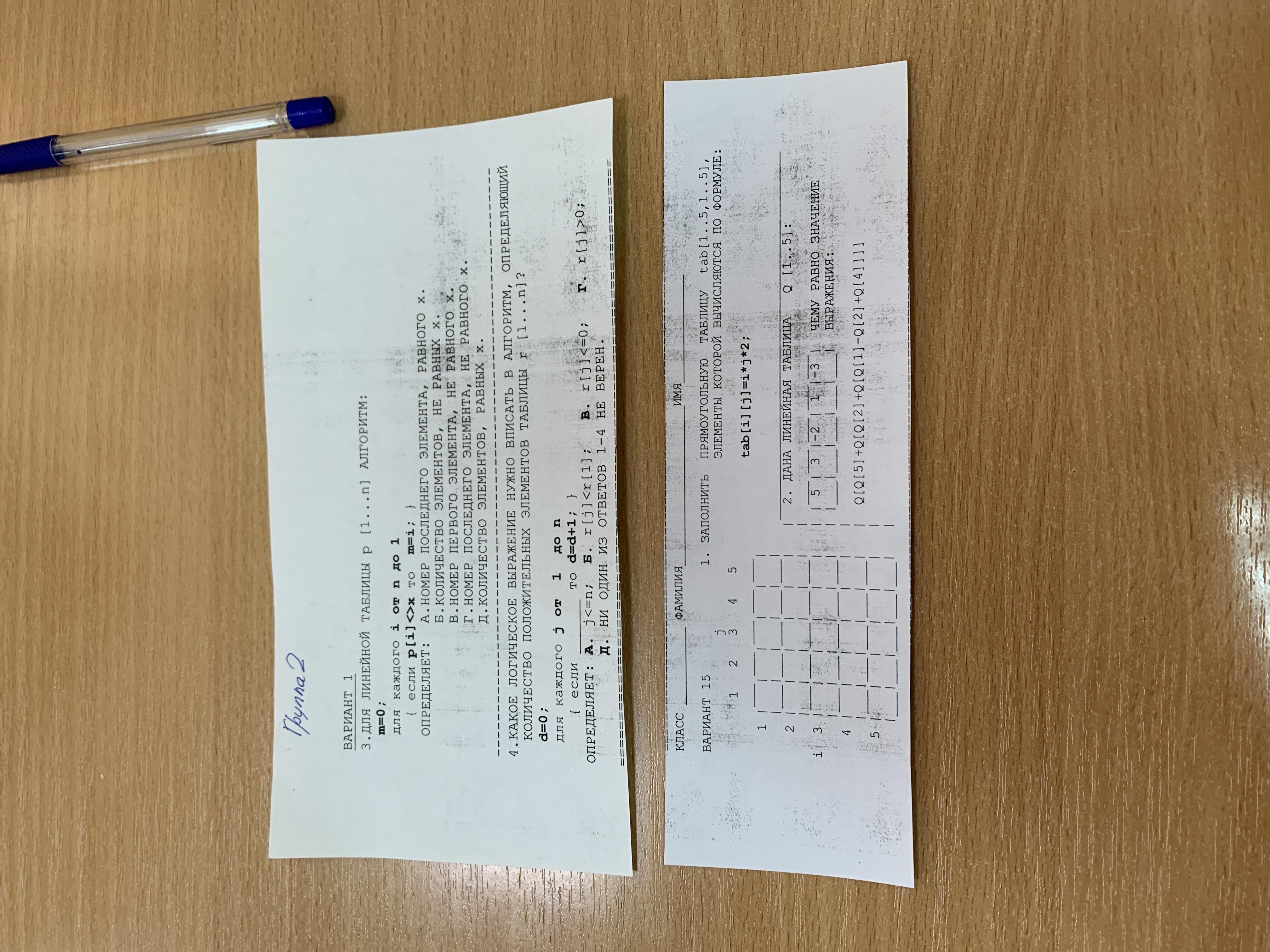
Верхний лист:
3) Г
4) Г
Нижний лист:
1)     2   4    6     8    10
      4   8    12    16   20
      6   12   18    24  30
      8   16   24   32  40
     10   20  30  40  50
2) Q[2] = 3

Объяснение:
Верхний лист:
3) Цикл p[i] != x итерируется по массиву от 1 до n, без условия
   break\continue, значит цикл в любом случае будет пройден до
   конца, то есть, это в любом случае будет ПОСЛЕДНИЙ элемент
   (варианты А или Г), осталось только посмотреть на само условие.
   при котором m = i, в нашем случае это условие неравенства икс
   i <>  x (тоже самое что и i != x), так
   что вариант Г
4) Очевидный вариант Г, так как r это массив [1..n], а j это текущий
   индекс массива. Чтобы найти текущий элемент массива r
   используем запись r[j].  Теперь осталось найти только
   положительные элементы. Положительные, это те, что > 0, отсюда
   r[j] > 0, вариант Г
Нижний лист:
1) Это вложенные циклы. По сути выражение tab[i][j] = i*j*2 на каждой
  итерации внутреннего цикла генерирует ячейку таблицы умножения
  умноженную на 2. Простыми словами: это кусок таблицы умножения
  где каждая ячейка умножена на 2
2) q[q[5] + q[q[2] + q[q[1] - q[2] + q[4]]]]
   Сначала вычислим самую вложенную часть
   q[q[5] + q[q[2] + q[5 - 3 + 1]]]] => q[q[5] +q[q[2] + q[3]]]
   Затем
   q[q[5] + q[3 + (-2)]] => q[q[5] + q[1]]
   Остаётся
   q[-3 + 5] => q[2] => 3