МЕГА СРОЧНО!!!!!! ПОМОГИТЕ!!!!!!! МНОГО БАЛЛОВ!!!!!
Докажите, что сумма медиан треугольника меньше периметра, но больше полупериметра треугольника.

Ответ:

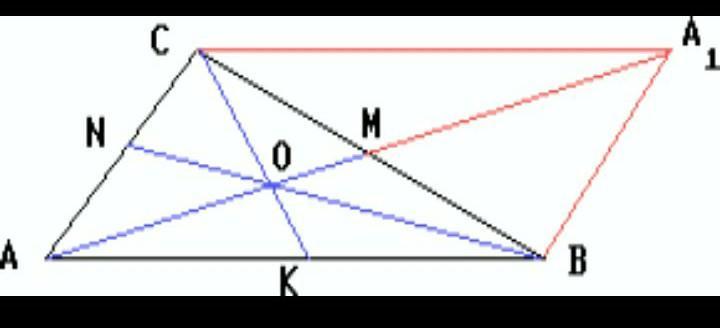
Отложим на продолжении медианы AM за точку M отрезок MA1, равный AM. Тогда ABA1C — параллелограмм (см рисунок)

Поэтому

BA1 = AC, 2AM = AA1 < AB + BA1 = AB + AC

Отсюда следует, что AM < 1/2(AB + BC).

Аналогично докажем, что

BN < 1/2(AB + BC),

CK < 1/2(AC + BC).

Сложив почленно эти три неравенства, получим:

AM + BN + CK < AB + BC + AC.