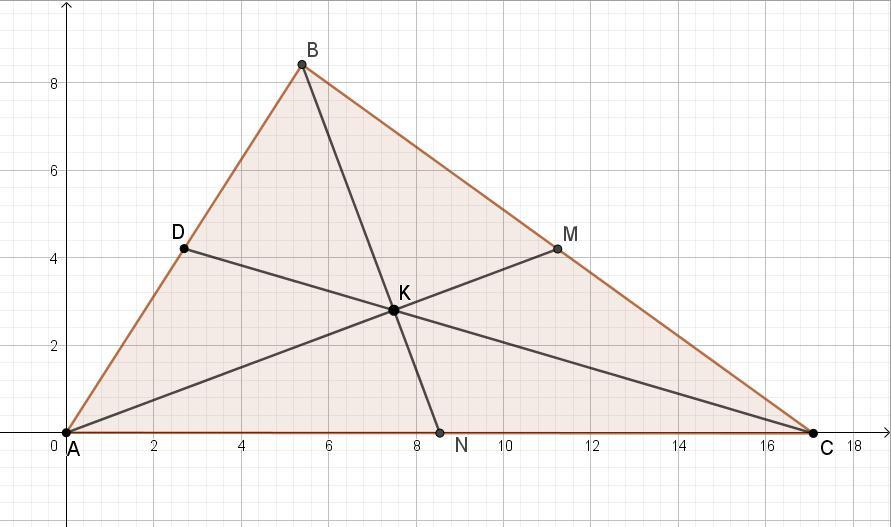
медианы am и bn треугольника abc перпендикулярны и пересекаются в точке k. найдите длину медианы am, если ck=10, bn=9​

Надо воспользоваться свойством медиан треугольника:

сумма квадратов медиан произвольного треугольника составляет 3/4 от суммы квадратов его сторон.

Если отрезок СК медианы равен 10, то сама медиана равна 15.

Примем отрезок КМ = х, тогда медиана АМ = 3х.

На основе условия задания, что медианы АМ и BN перпендикулярны, найдём длины сторон.

АВ² = 4х² + 36,

ВС² = 4(36 + х²),

АС² = 4(4х² + 9).

Применим свойство:

(3х)² + 9² + 15² = (3/4)( 4х² + 36 +  4(36 + х²) + 4(4х² + 9)).

Получаем 9х² = 144 или х² = 16, отсюда х = 4.

Ответ: медиана АМ = 3*4 = 12.