Математика, вопрос задал 0001001 , 2 года назад

математика. помогите, пожалуйста, с заданиями 3-5

Приложения:

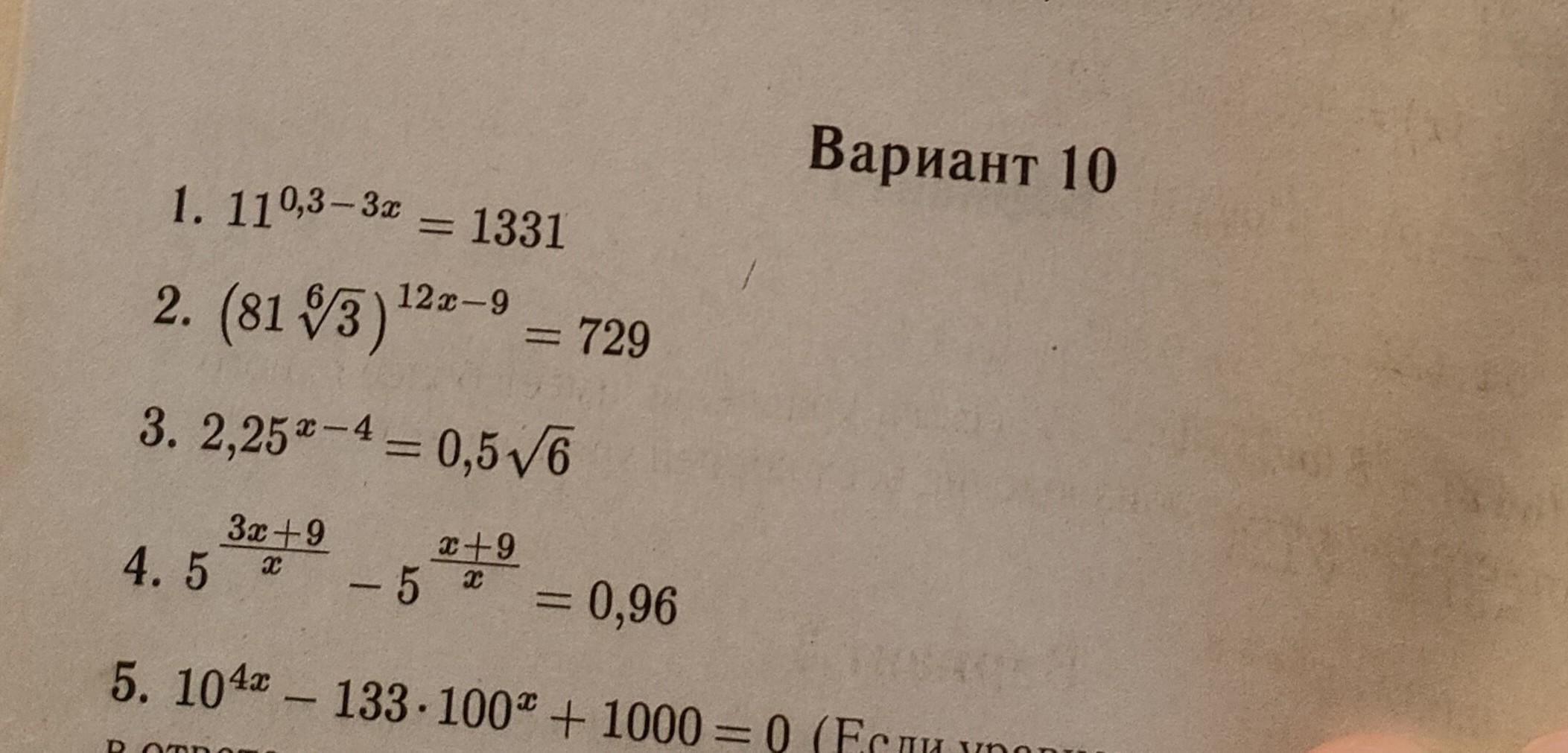
Ответы на вопрос

Ответил NNNLLL54

Ответ:

$3)\ \ 2,25^{x-4}=0,5\sqrt6$

Заметим, что $2,25=\dfrac{225}{100}=\dfrac{15^2}{10^2}=\Big(\dfrac{15}{10}\Big)^2=\Big(\dfrac{3\cdot 5}{2\cdot 5}\Big)^2=\Big(\dfrac{3}{2}\Big)^2$ и

$0,5\sqrt6=\dfrac{1}{2}\cdot \sqrt6=\dfrac{\sqrt6}{2}=\dfrac{\sqrt2\cdot \sqrt3}{(\sqrt2)^2}=\dfrac{\sqrt3}{\sqrt2}$ .

$\left(\Big(\dfrac{3}{2}\Big)^2\right)^{x-4}=\dfrac{\sqrt3}{\sqrt2}\ \ ,\ \ \ \ \Big(\dfrac{3}{2}\Big)^{2x-8}=\Big(\dfrac{3}{2}\Big)^{\frac{1}{2}}\ \ \ \ \Rightarrow \ \ \ 2x-8=\dfrac{1}{2}\ \ ,\\\\\\2x=8,5\ \ ,\ \ \boxed{\bf x=4,25\ }$

$4)\ \ 5^{\frac{3x+9}{x}}-5^{\frac{x+9}{x}}=0,96\\\\5^{3+\frac{9}{x}}-5^{1+\frac{9}{x}}=0,96\ \ ,\ \ \ \ 5^3\cdot 5^{\frac{9}{x}}-5\cdot 5^{\frac{9}{x}}=\dfrac{96}{100}\ \ ,\ \ \ 5^{\frac{9}{x}}\cdot (5^3-5)=\dfrac{24}{25}\ ,\\\\5^{\frac{9}{x}}\cdot 120=\dfrac{24}{25}\ \ ,\ \ \ 5^{\frac{9}{x}}=\dfrac{24}{25\cdot 120}\ \ ,\ \ \ \ 5^{\frac{9}{x}}=\dfrac{1}{25\cdot 5}\ \ ,\ \ \ 5^{\frac{9}{x}}=\dfrac{1}{5^3}\ ,\ \ 5^{\frac{9}{x}}=5^{-3}$

Приравниваем показатели степеней .

$\dfrac{9}{x}=-3\ \ ,\ \ \ x=-\dfrac{9}{3}\ \ ,\ \ \ \ \boxed{\bf \ x=-3\ }$

$5)\ \ 10^{4x}-133\cdot 100^{x}+1000=0$

Заметим, что $10^{4x}=10^{2\cdot 2x}=(10^2)^{2x}=100^{2x}=(100^{x})^2$

$(100^{x})^2-133\cdot 100^{x}+10000=0$

Замена переменных: $t=100^{x} > 0\ \ ,\ \ t^2-133\, t+1000=0\ \ ,$

$D=133^2-4\cdot 1000=17689-4000=13689=117^2\\\\t_1=\dfrac{133-117}{2}=8\ \ ,\ \ \ t_2=\dfrac{133+117}{2}=125$

Переходим к старой переменной .

$a)\ \ 100^{x}=8\ \ \Rightarrow \ \ \ 10^{2x}=8\ \ ,\ \ \ 2x=log_{10}\, 8=lg2^3=3\, lg2\ \ ,\\\\ x=\dfrac{3}{2}\, lg2=lg2^{\frac{3}{2}}\ \ ,\ \ \ x=lg\sqrt{2^3}\ \ ,\ \ \boxed{\bf \ x=lg(2\sqrt2)\ }$

$b)\ \ 100^{x}=125\ \ \Rightarrow \ \ \ 10^{2x}=125\ \ ,\ \ \ 2x=log_{10}\, 125=lg5^3=3\, lg5\ \ ,\\\\ x=\dfrac{3}{2}\, lg5=lg5^{\frac{3}{2}}\ \ ,\ \ x=lg\sqrt{5^3}\ \ ,\ \ \ \ \boxed{\bf \ x=lg(5\sqrt5)\ }$