математика даю 40 баллов​

Ответ:

a = 1

Пошаговое объяснение:

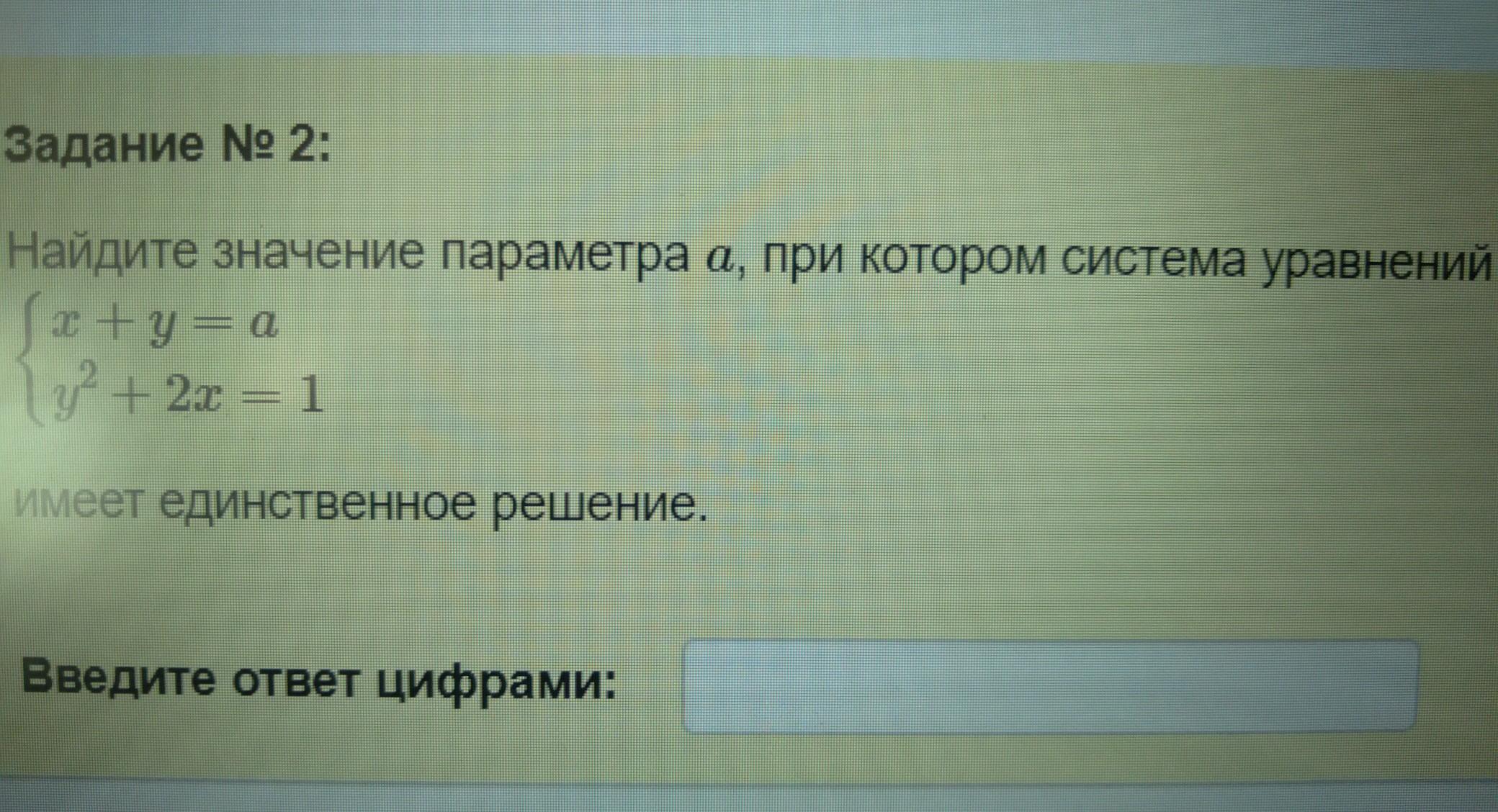
В первом уравнении выразим x и подставим во второе:

Необходимое условие для того, чтобы система имела только одно решение - чтобы у второго уравнения было только 1 решение. То есть его дискриминант должен быть равен нулю.

Необходимое условие: a = 1.

Проверка:

Имеется единственное решение, a = 1 - ответ