Квадрат и прямоугольник, площади которых соответственно равны 36см² и 96см²,имеют общую сторону ,а расстояние между их параллельными сторонами равно 14 см.Найдите угол между плоскостями квадрата и прямоугольника.(C рисунком,зарание спасибо)
Ответы на вопрос
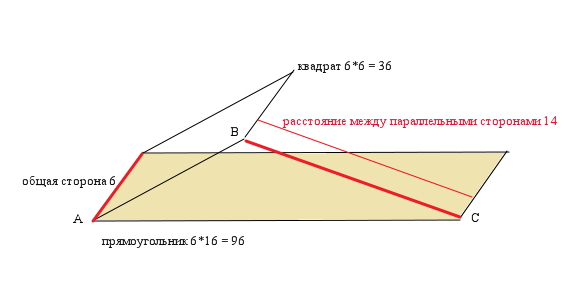
угол между плоскостями квадрата и прямоугольника ---это угол BAC на рисунке
(т.к. АВ _|_ их общей стороне---как стороны квадрата и АС _|_ их общей стороне---как стороны прямоугольника...)
в треугольнике BAC все стороны известны: АВ---сторона квадрата = 36 = 6*6 => общая сторона = 6
АС---сторона прямоугольника = 96/6 = 16
ВС = 14
по т.косинусов: 14^2 = 6^2 + 16^2 - 2*6*16*cos(BAC)
12*16*cos(BAC) = 36 + 16^2 - 14^2 = 36 + (16-14)(16+14) = 36 + 2*30 = 36+60 = 96
cos(BAC) = 96 / (12*16) = 6/12 = 1/2
угол ВАС = 60 градусов
Угол ACM - угол между плоскостями квадрата BACD и прямоугольника DCMN.
АС =√36= 6 см, СМ =96:6=16 см, АМ =14 см (по усл).
По т косинусов cos ACM =(256+36-196)/2·6·16 =0,5, Угол ACM равен 60°
