Кут між площиною многокутника і її проекцією 45°, площа проекції 10 см2 Знайти площу многокутника у просторі​

Ответ:

Площа многокутника дорівнює 10√2 см²

Объяснение:

Кут між площиною многокутника і її проекцією 45°, площа проекції 10 см². Знайти площу многокутника у просторі.

• Площа ортогональної проекції многокутника дорівнює добутку площі многокутника на косинус кута між площинами многокутників.

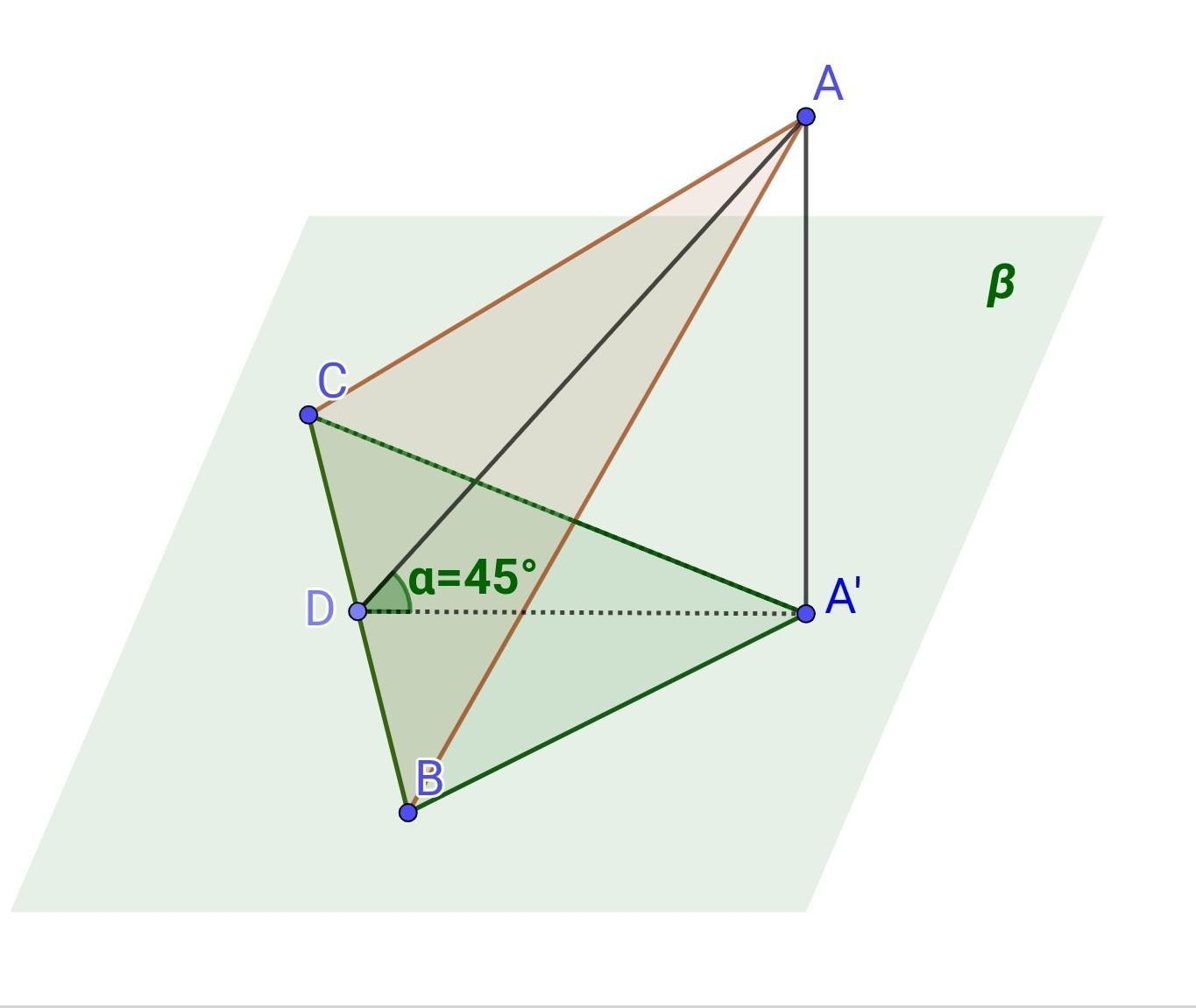
Якщо △А'ВС - ортогональна проекція △АВС на площину ß, то:

S(△A'BC) = S(△ABC) • cosα

За умовою, S(△A'BC) = 10 см², кут α = 45°, тоді площа многокутника у просторі:

(см²).

Отже, площа многокутника у просторі дорівнює 10√2 см².

#SPJ1