Кто решит хотя бы одно, спасибо вам большое, просто прикрепил все сразу чтобы было удобнее. Всем заранее спасибо за помощь!
Приложения:
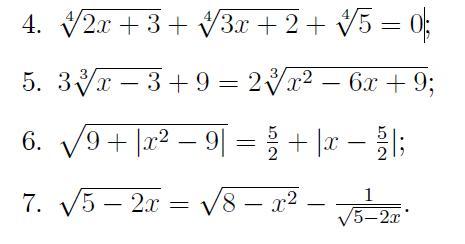
viktorfedotov334:
понимаю что не программа 9 класса а чуть дальше, но а что делать
Специалисты в помощь: NNNLLL54
• главный мозг
• 34.1 тыс. ответов
• 185.8 млн пользователей, получивших помощь
https://znanija.com/app/profile/1385058
m11m
• главный мозг
• 17.7 тыс. ответов
https://znanija.com/app/profile/4346812/answers
Simba2017
https://znanija.com/app/profile/9971431/answers
https://znanija.com/app/profile/16764525/answers
• главный мозг
• 34.1 тыс. ответов
• 185.8 млн пользователей, получивших помощь
https://znanija.com/app/profile/1385058
m11m
• главный мозг
• 17.7 тыс. ответов
https://znanija.com/app/profile/4346812/answers
Simba2017
https://znanija.com/app/profile/9971431/answers
https://znanija.com/app/profile/16764525/answers
ух ты, спасибо
поищу решения там...
))
Ответы на вопрос
Ответил sofiyavictoria
5
Ответ:
х1=30, х2= -3/8
Пошаговое объяснение:
5. 3∛(х-3)+9=2∛(x^2-6x+9)
2∛(x-3)^2-3∛(x-3)-9=0 Введем вспомогательную переменную.
Пусть ∛(х-3)=t. Тогда получим уравнение
2t^2-3t-9=0. D=9+4*2*9=9+72=81. t1=(3+9)/4=3, t2=(3-9)/4= -6/4= -3/2.
Вернемся к исходной переменной
∛(х-3)=3. Возведем обе части уравнения в куб. х-3=27. х1=27+3. х1=30
∛(х-3)= -3/2. х-3= -27/8. х-3= -3 3/8 . х2= -3 3/8+3. х2= -3/8
Спасибо большое
52628399373833
Ответил NNNLLL54
6
Ответ.
Корни чётных степеней принимают неотрицательные значения, значит
. Сумма этих трёх корней
четвёртой степени точно будет больше 0 , и равняться 0 не может.
Уравнение не имеет решений при любых значениях переменной, входящих в ОДЗ.
Новые вопросы
Қазақ тiлi,
1 год назад
Математика,
8 лет назад