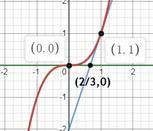
Кто нибудь Помогите пожалуйста! Уже который день мучаюсь!!! Найдите объем фигуры, образованной вращением вокруг оси Ох криволинейной трапеции, ограниченной графиком функции у = х^3, касательной к этому графику в точке с абсциссой х0 = 1 и прямой у = 0.
Ответ: 2π/63. Как его получили?​

Ответ:

Пошаговое объяснение:

уравнение касательной в точке х₀ = 1  будет

y' = (x³)' = 3x²

y(x₀) = 1

y'(x₀) = 3

или

y = 3x-2

теперь ищем точку пересечения касательной и  у=0

это будет 3х-2 =0⇒  х=2/3

теперь к объему

мы будем считать разность объемов тела, ограниченного у=х³ и у=0 (V₁) (от 0 до 1 по х)

и тела ограниченного у= 3х-2 и у=0     (V₂) (от 2/3 до 1 по х)

здесь замена и пересчет пределов интегрирования

u = 3x-2; du=3dx; нижний предел u=0; верхний предел u=1

и тогда получим интеграл

и вот теперь

что и требовалось доказать....