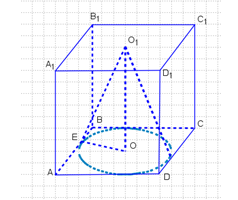
Конус, высота которого OO 1 =10 cm , вписан в куб. Вычислите объёмы конуса и куба.
Приложения:
Ответы на вопрос
Ответил 2Stupid
0
Объём куба найдем по формуле:
 , где a = AD = DD1 - ребро куба.
, где a = AD = DD1 - ребро куба.
OO1 = DD1 = 10 см.

Объем конуса найдем по формуле:
 , где R - радиус основания конуса, а H - высота конуса, которая равна боковому ребру куба, то есть H = DD1 = 10.
, где R - радиус основания конуса, а H - высота конуса, которая равна боковому ребру куба, то есть H = DD1 = 10.
Радиус основания конуса, вписанного в куб, равен:
 , где a - ребро куба.
, где a - ребро куба.

Найдем объем конуса:

Ответ: и
и 
OO1 = DD1 = 10 см.
Объем конуса найдем по формуле:
Радиус основания конуса, вписанного в куб, равен:
Найдем объем конуса:
Ответ:
Новые вопросы