Алгебра, вопрос задал RdBlackFox , 6 лет назад

Комбинаторика 1)Вычислите:

Приложения:

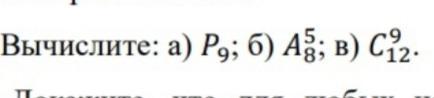
Ответы на вопрос

Ответил Vopoxov

Ответ:

$P_9=362\,880\\A_8^5=336\\C_{12}^9=220$

Объяснение:

$P_n$ - это число перестановок из n, вычисляется как

$P_n=n!=1\cdot2\cdot...\cdot{n}$

$P_9=9!=1{\cdot}2{\cdot}3{\cdot}4{\cdot}5{\cdot6}{\cdot}7{\cdot8\cdot}9 = \\ = (1{\cdot}2{\cdot}3{\cdot}4{\cdot}5{\cdot6}){\cdot}(7{\cdot8\cdot}9 ) = 720{\cdot}504 = \\ = 362 \: 880$

$A_n^k$ - это число размещений из n по k; вычисляется как

$A_n^k=\frac{n!}{k!}=\frac{1\cdot2\cdot...\cdot{n}}{1\cdot2\cdot...\cdot{k}}$

$A_8^5=\frac{8!}{5!}= \small{\frac{ \cancel{1\cdot2\cdot3\cdot4\cdot5 \: } {\cdot} \: 6\cdot7\cdot{8}}{ \cancel{1\cdot2\cdot3\cdot4\cdot{5}}} =} \\ = 6\cdot7\cdot{8} = 336$

$C_n^k$ - это число сочетаний из n по k; вычисляется как

$C_n^k=\frac{n!}{k!(n - k)!}=\frac{1\cdot2\cdot...\cdot{n}}{(1\cdot2\cdot...\cdot{k}) \cdot(1\cdot2\cdot...\cdot({n{ - }k}))}$

$C_{12}^9=\frac{12!}{9!(12 - 9)!}= \\ = \frac{ \cancel{1\cdot2\cdot... \cdot9}\cdot10\cdot11\cdot{12}}{ \cancel{(1\cdot2\cdot...\cdot{9})} \cdot(1\cdot2\cdot3)} = \\ = \frac{10\cdot11\cdot12}{1\cdot2\cdot3} = \frac{1320}{6} = 220$

Предыдущий вопрос

Следующий вопрос

Новые вопросы

История, 1 год назад

Перечислить руководителей России и ссср с 1917 года помогите прошу...

Физика, 1 год назад

Обмотки катушек понижающего трансформатора содержат 150 и 60 витков соответственно. Какое напряжение снимают со вторичной обмотки, если трансформатор включён в сеть с напряжением 220 В?

Математика, 6 лет назад

пппппппппжжжжжжжжжжжж...

Биология, 6 лет назад

функция липидов в клетке пожалуйста помогите ...

Математика, 8 лет назад

Запишите все двузначные числа , в записи которых используются только цифры 2,4,9 и 0.(цифры могут повторяться).

История, 8 лет назад

Что значит быть моральным?