Коло з діаметром АВ задано рівнянням (х + 2)2 + (y -2)2=16. Знайдіть координати точки В, якщо: а) А(2; 2); 6) А(-2; 6). Даю 97 балов
срочьно

Ответ:

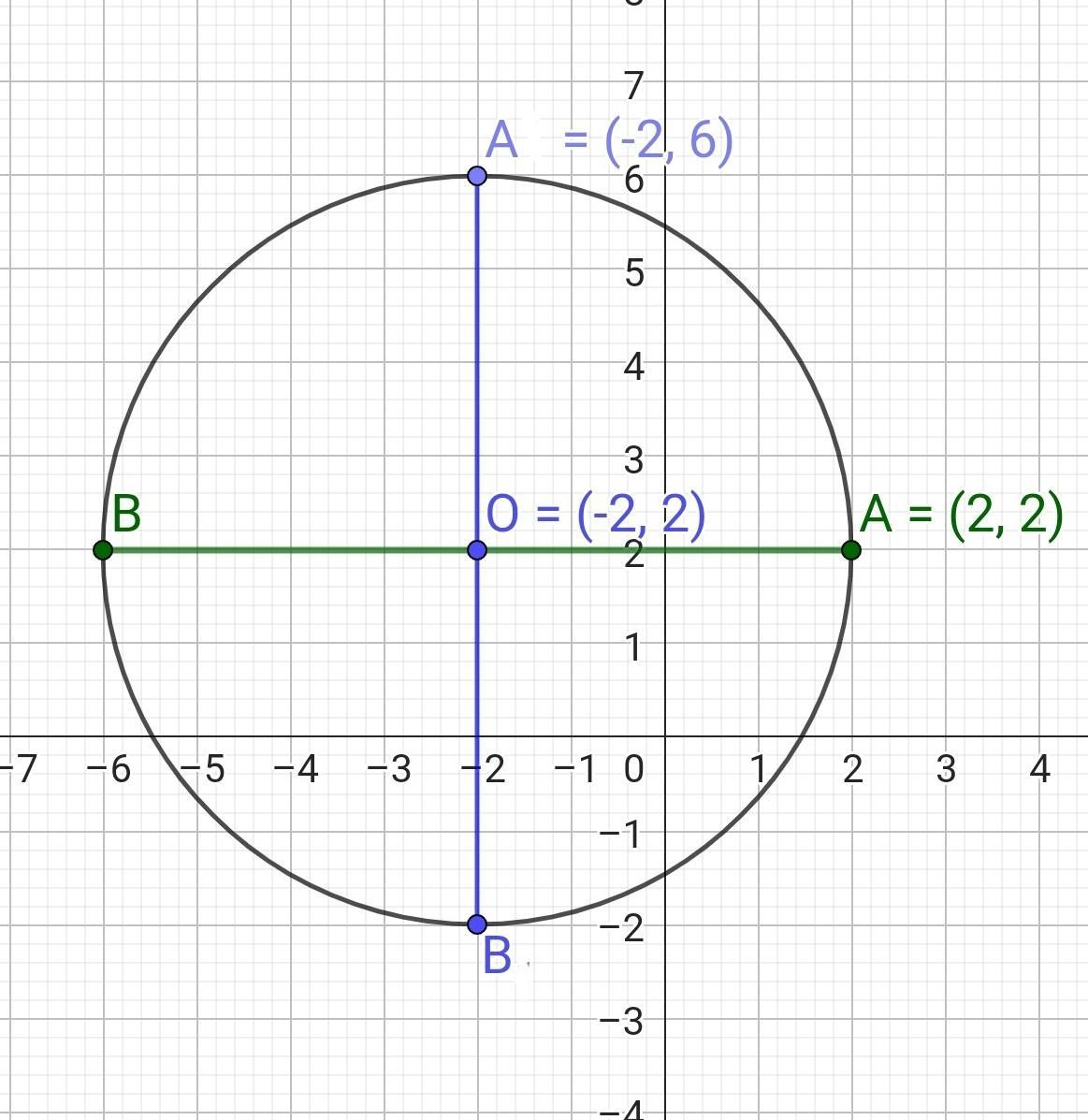
а) В(-6; 2)

b) В(-2; -2)

Объяснение:

Коло з діаметром АВ задано рівнянням (х + 2)² + (y -2)²=16. Знайдіть координати точки В, якщо: а) А(2; 2); 6b) А(-2; 6).

Рівняння кола з центром у точці (a;b) і радіусом r має вигляд:

(x-a)²+(y-b)²=r²

Тоді:

(x + 2)² + (y − 2)² = 16;

(x + 2)² + (y − 2)² = 4²

Центр кола у точці O(-2; 2), радіус кола r = 4.

• Діаметр кола - це відрізок, що сполучає дві точки кола та проходить через центр кола.

Отже, О(-2;2) - середина відрізка АВ.

Із умови, що АО=ОВ складаємо рівняння для знаходження координати точки В і розв'язуємо.

a) A(2; 2)

B(-6; 2)

b) A(-2; 6)

B(-2; -2)

#SPJ1