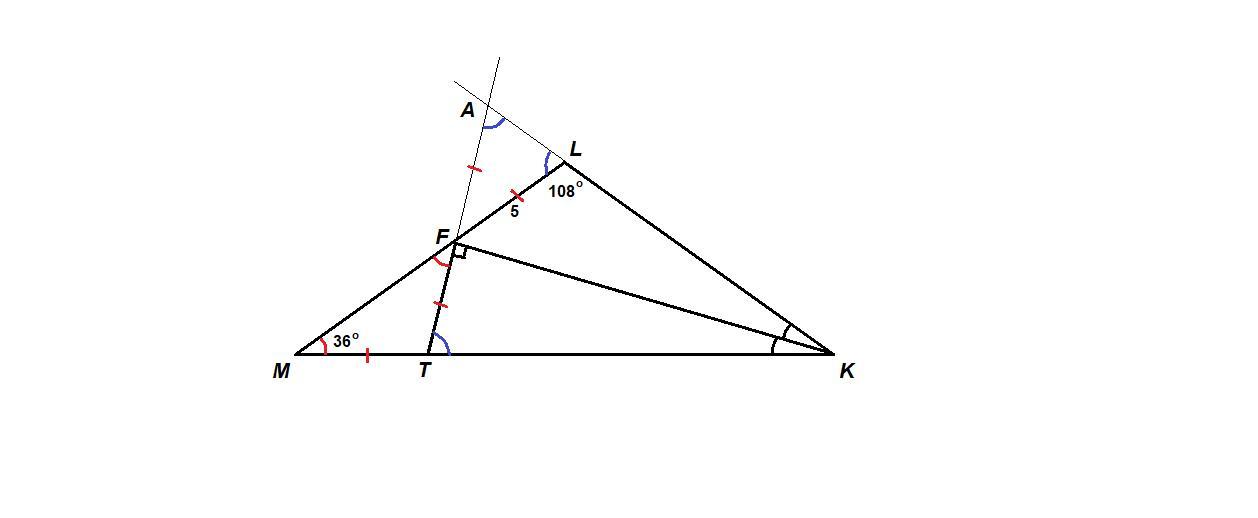
KF - биссектриса треугольника KLM, в котором KLM — 108°.
LMK — 36°. Точка T лежит на стороне КМ. и при этом TFK = 90°.
Найдите TM, если LF — 5.
Указание. Продлите TF и KL до пересечения в точке А.
dashunina2005:
Школа при мфти?
да
А где решение?
давался месяц, а спрашивают только сейчас, логика)
Ответы на вопрос
Ответил KuOV
0
Ответ:
5
Объяснение:
Из ΔКLM:
∠LKM = 180° - (∠KLM + ∠LMK) = 180° - (108° + 36°) = 180° - 144° = 36°
Продлим TF и KL до пересечения в точке А.
KF - биссектриса и высота в ΔАТК, значит он равнобедренный,
∠КАТ = ∠КТА = (180° - ∠LKM)/2 = (180° - 36°)/2 = 72°
∠FLA = 180° - ∠KLM = 180° - 108° = 72° (смежные углы), ⇒
ΔFAL - равнобедренный, AF = FL = 5.
__________________________________
TF = AF = 5, так как KF и медиана равнобедренного треугольника АКТ.
__________________________________
∠KTF - внешний для ΔTMF, значит равен сумме двух внутренних, не смежных с ним:
∠KTF = ∠TMF + ∠TFM
∠TFM = ∠KTF - ∠TMF = 72° - 36° = 36°, значит
ΔTMF равнобедренный, TM = FT = 5
Приложения:
Новые вопросы