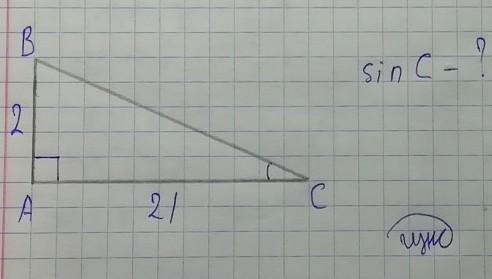
Катет прямого треугольника равен 21 и 2. Найдите синус наименьшего угла этого треугольника
Ответы на вопрос
Ответил Nekit455
0
По теореме Пифагора найдем гипотенузу
BC² = AB² + AC²
BC² = 4 + 441 = 445
BC = √445
Теорема: против меньшей стороны лежит меньший угол.
Отсюда делаем вывод, что меньший из острых углов прямоугольного треугольника будет ∠C (лежит напротив меньшего катета AB, равному 2 ед.)
Синус - отношение противолежащего катета к гипотенузе

BC² = AB² + AC²
BC² = 4 + 441 = 445
BC = √445
Теорема: против меньшей стороны лежит меньший угол.
Отсюда делаем вывод, что меньший из острых углов прямоугольного треугольника будет ∠C (лежит напротив меньшего катета AB, равному 2 ед.)
Синус - отношение противолежащего катета к гипотенузе
Приложения:
Новые вопросы