Физика, вопрос задал alexandrarenino , 2 года назад

Какой должен быть радиус выпуклого моста, имеющего вид дуги
окружности, если вес автомобиля, движущегося со скоростью 36 км/ч,
в верхней части моста уменьшился вдвое. Принять g = 10 м/с2.

Приложения:

K4R4Nora: 20 будет

Ответы на вопрос

Ответил VоЛk

Дано:

v = 10 м/с

g = 10 м/с²

P₁ = 2P₂

R - ?

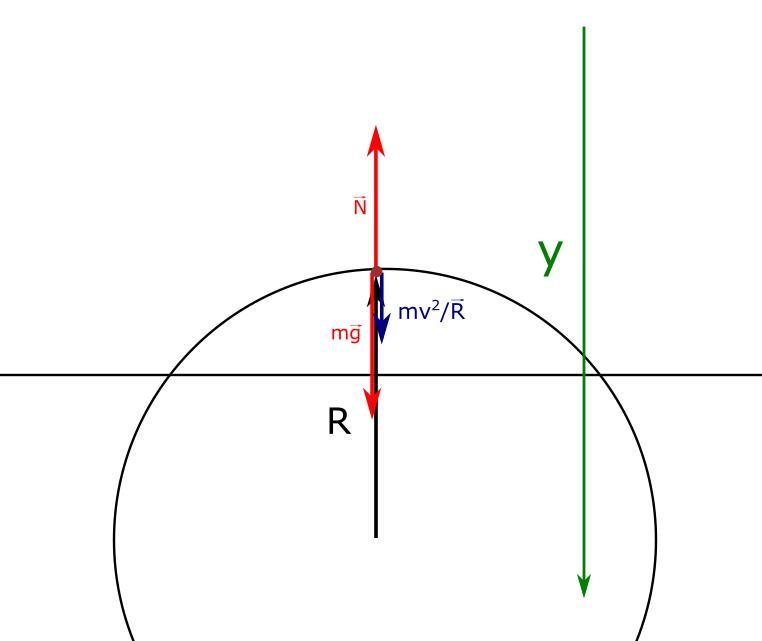
На автомобиль, двигающегося по окружности, помимо силы тяжести и силы реакции опоры, действует центростремительная сила.

Запишем второй закон Ньютона для тела и спроецируем его на ось у.

$m\vec{a} = m\vec{g} + \vec{N} + \dfrac{mv^2}{\vec{R}}\\\\Oy:ma = \dfrac{mv^2}{R}\\a = \dfrac{v^2}{R}$

Сила тяжести компенсируется силой реакции опоры

Значит, тело движется с ускорением v²/R к центру окружности.

Из формулы веса тела, которое движется с ускорением:

$\vec{P} = m(\vec{g} - \vec{a})\\Oy: P_2= m(g-a) \\P_1 = mg\\mg = 2m(g - a) \\mg = 2mg - 2ma\\\dfrac{v^2}{R} = \dfrac{g}{2}\\R = \dfrac{2v^2}{g}\\R = 20 \\$

[R] = (м/с)² / (м/с²) = м

Ответ: 20 метров

Приложения:

Предыдущий вопрос

Следующий вопрос

Новые вопросы

Немецкий язык, 1 год назад

Помогите очень нужно...

Английский язык, 1 год назад

Напишите перевод с русского на английский: костюм с помощью которого можно развивать сверхзвуковую скорость. Люди могли бы передвигаться очень быстро,и быть,где захотят...

Английский язык, 2 года назад

They ___(visit) their parents next yeariv болымды және болымсыз ...