какое задание? надо решить неравенство, но я прошу вас только проверить.
неравенство (x + 3)(x - 9) > 0
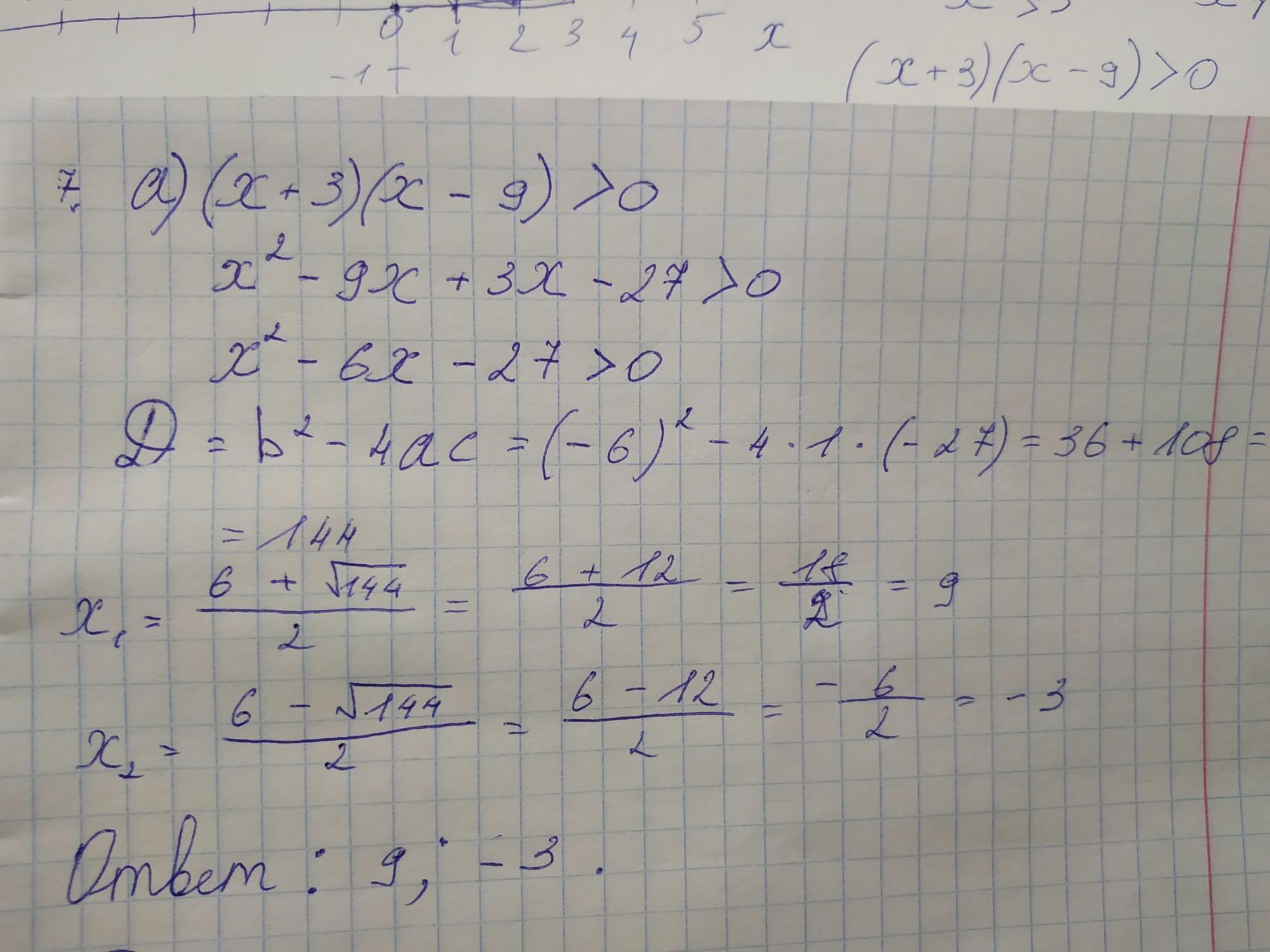
Ответы на вопрос
Ответ:
в точках 9 и минус 3 функция равна нулю.
для того чтобы решить неравенство, не нужно было раскрывать скобки и искать дискриминант.
произведение равно нулю, тогда когда один из его множителей равен нулю
для того чтобы найти где больше нуля. для этого на числовой прямой отметим нули функции.
это -3 и 9
таким образом, получим три интервала.
(-беск.;-3)(-3;9)(9;+беск.)
таким образом, ветви функции направлены вверх. следовательно больше нуля получим крайние интервалы.
+ - +
ответ (-беск.;-3)(9;+беск.)
Нет, к сожалению, решается это задание, например, с помощью метода интервалов. Вы сделали двойную работу, раскрыли скобки, а потом нашли корни левой части. Это можно было сделать, не прибегая к решению квадратного уравнения, а просто приравнять к нулю сначала одну, потом другую скобки, итак, корни найдены. Это -3 и 9. Разбиваем ими числовую ось на интервалы (-∞;-3);(-3;9);(9;+∞), и устанавливаем знак на каждом промежутке, для чего можете просто подставить число из данного интервала и узнать знак левой части неравенства. Например, на промежутке (-∞;-3) берем -4
Подставляем в левую часть неравенства, получаем (-4+3)(-4-9)
и видим, что знак там в первой скобке минус и во второй минус, а минус на минус даст плюс, аналогично во втором интервале получим минус, и в третьем плюс. Нас интересуют плюсы. Поэтому ответом будет объединение промежутков (-∞;-3)∪(9;+∞)