Математика, вопрос задал Veniz , 2 месяца назад

Как решить этот пример 2cos3x-1<0

Ответы на вопрос

Ответил Artem112

0

Ответ:

$\dfrac{\pi }{9} +\dfrac{2\pi n}{3} < x < \dfrac{5\pi }{9} +\dfrac{2\pi n}{3} ,\ n\in\mathbb{Z}$

Решение:

$2\cos3x-1 < 0$

$2\cos3x < 1$

$\cos3x < \dfrac{1}{2}$

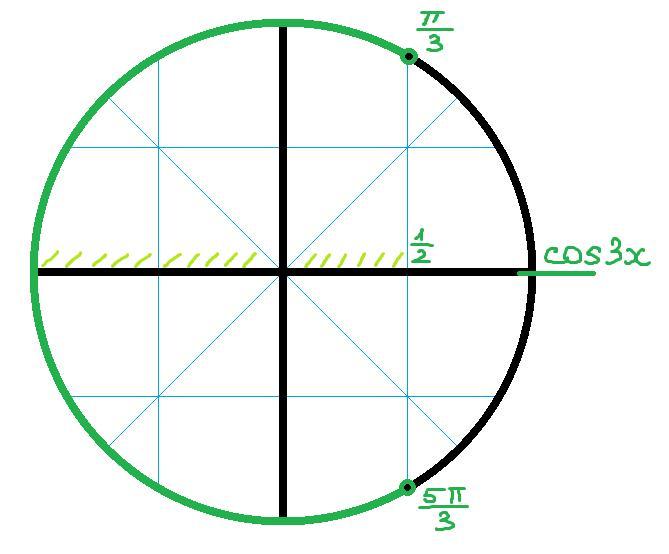
Решение на тригонометрической окружности относительно угла $3x$ показано на картинке.

$\arccos\dfrac{1}{2} +2\pi n < 3x < 2\pi-\arccos\dfrac{1}{2} +2\pi n$

$\dfrac{\pi }{3} +2\pi n < 3x < \dfrac{5\pi }{3} +2\pi n$

Разделим на 3 все части неравенства:

$\boxed{\dfrac{\pi }{9} +\dfrac{2\pi n}{3} < x < \dfrac{5\pi }{9} +\dfrac{2\pi n}{3} ,\ n\in\mathbb{Z}}$

Приложения:

Предыдущий вопрос

Следующий вопрос

Новые вопросы

Экономика, 2 месяца назад

Завдання Завдання 3.3. Визначити чисельність працюючих в звітному періоді, якщо відомо, що випуск продукції в звітному періоді зросте в порівнянні з базисним на 8%, а продуктивність праці...

Физика, 2 месяца назад

ЧЕКАЮ ЛЮДИНУ ЯКА ДОПОМОЖЕ ДУУУУЖЕЕЕ ПРОШУУУ...

Физика, 2 месяца назад

1. Ядро якого елемента утворилося після β-розпаду атома Актинію (89 Ас 235)? 2. Ядро атома Бісмуту (94 Ві 244) зазнало 1α-розпад і далі 2 β-розпади. Ядро якого елементу утворилося?

Математика, 2 месяца назад

8. Двум автомобилям необходимо проехать из города А в город Б, расстояние которого составляет 840 км, и одна из машин преодолевает это расстояние менее чем за 2 часа. За это время первый автомобиль...

Русский язык, 6 лет назад

Помогите пожалуйста. Определите тему данного отрывка из "Уроки французского". Голод здесь совсем не походил на голод в деревне. Там всегда, и особенно осенью, можно было что-то перехватить,...

Английский язык, 6 лет назад

Помогите пожалуйста дз по английскому языку 5 решите ок...