Математика, вопрос задал dd202046 , 1 год назад

Как решить данное выражение?

Приложения:

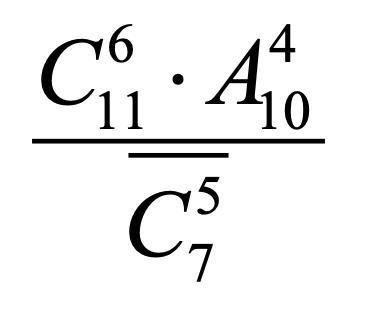
Ответы на вопрос

Ответил himikomat

Ответ:

$\frac{C_{11} ^{6} \times A_{10} ^{4} }{ C_{7} ^{5} }$

$\frac{ \frac{11!}{6! \times (11 - 6)!} \times{ A_{10} ^{4} } }{ \frac{7!}{5! \times (7 - 5)!} }$

$\frac{ \frac{11 \times 10 \times 9 \times 8 \times 7 \times 6!}{6! \times 5!} \times{ A_{4} ^{10} } }{ \frac{7 \times 6 \times 5!}{5! \times 2!} }$

сокращаем на общие делители 6! и 5!:

$\frac{ \frac{11 \times 10 \times 9 \times 8 \times 7}{5!} \times{ A_{10} ^{4} } }{ \frac{7 \times 6}{2!} }$

$\frac{ \frac{55440}{120} \times{{{A}_{10}^{4}}} }{ \frac{42}{2} }$

сокращаем на общий делитель 120 и общий делитель 2:

$\frac{462 \times {{A}_{10}^{4}}}{21}$

сокращаем на общий делитель 21:

$22 \times {{A}_{10}^{4}}$

Новые вопросы

Математика, 1 год назад

Математика, 1 год назад

Биология, 1 год назад

Математика, 1 год назад

Геометрия, 6 лет назад

Геометрия, 6 лет назад