как найти объем правильной 4-х угольной пирамиды, зная площадь диагонального сечения?
Аноним:
Никак, нужны ещё данные.
Задание звучит так : Диагональное сечение правильной четырехугольной пирамиды представляет собой прямоугольный треугольник площадью 24 см2. Рассчитайте объем пирамиды!
Это же другое дело.
надеюсь, поможете
Подождите я рисунок делаю.
спасибо!
Ответы на вопрос
Ответил Аноним
1
Ответ:
32√6см³
Объяснение:
Дано:
SABCD- пирамида.
ABCD- квадрат.
SA=SB=SC=SD.
S(∆ASC)=24см²
<АSC=90°
V=?
_________
Решение
∆АSC- прямоугольный, равнобедренный.
AS=SC
S(∆ASC)=AS*SC/2
AS=√(2*S(∆ASC))=√(2*24)=4√3 см
SC=4√3 см
По теореме Пифагора
АС=√(AS²+SC²)=√(48+48)=√96=4√6см.
АВ=АС/√2=4√6/√2=4√3см.
S(ABCD)=AB²=(4√3)²=16*3=48см².
OC=AC/2=4√6/2=2√6см.
∆SOC- прямоугольный треугольник.
По теореме Пифагора
SO=√(SC²-OC²)=√((4√3)²-(2√6)²)=√(48-24)=
=√24=2√6см.
V=1/3*Sосн*Н=1/3*S(ABCD)*SO
V=1/3*48*2√6=32√6 см³
Приложения:
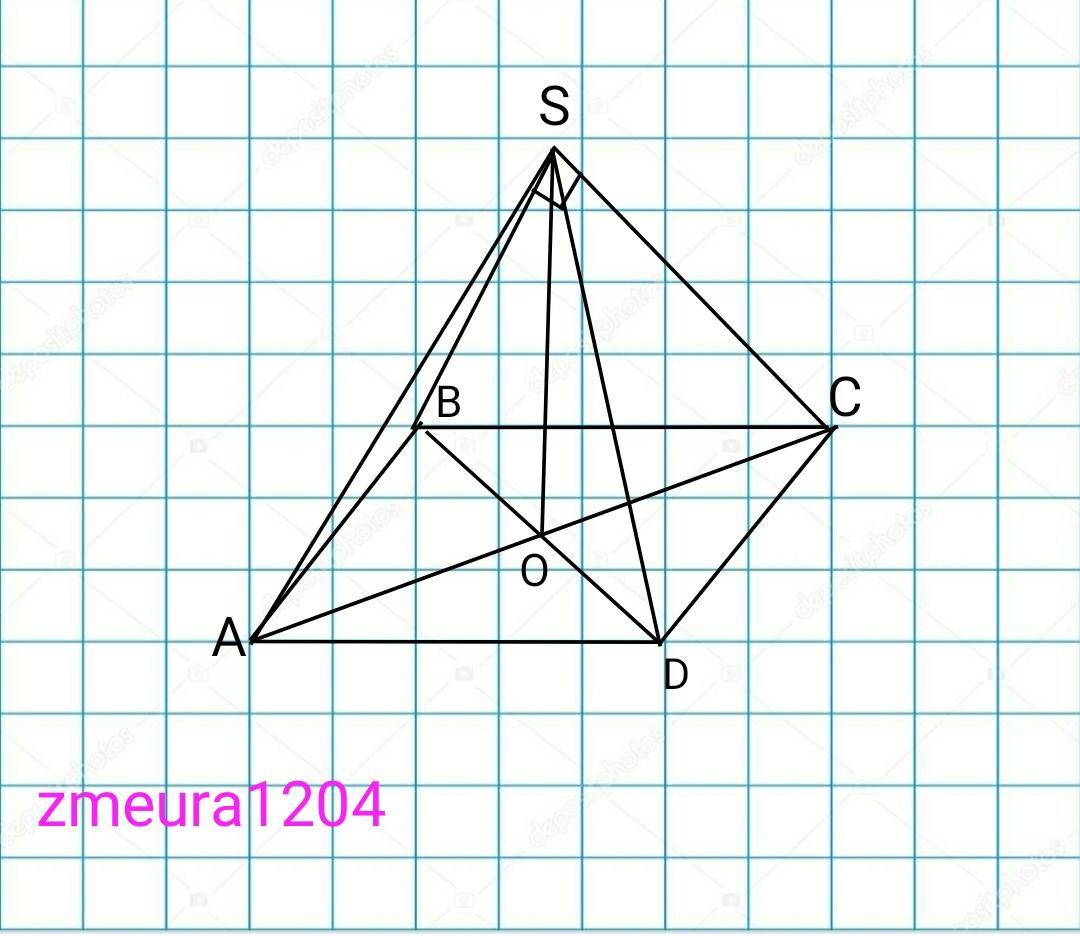
спасибо большое !!
Новые вопросы
Русский язык,
1 год назад
Биология,
2 года назад