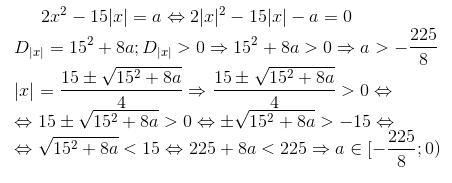Как можно быстрее, пожалуйста!(тому кто ответит-лучший ответ(жулью репорт!!!!))

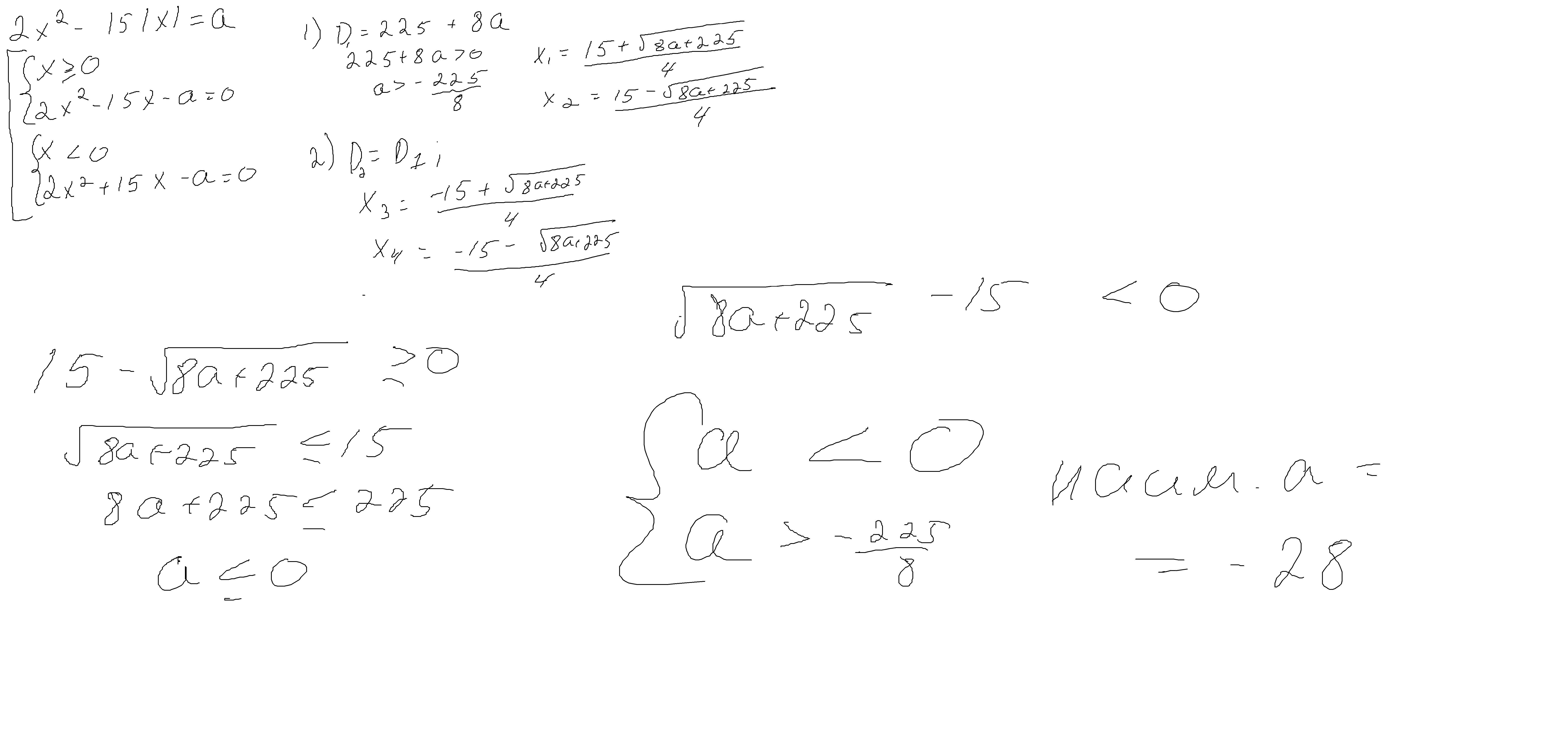
Находим дискриминант ,так как уравнение является квадратным относительно модуля,после чего надо нанести ограничение D>0,почему не равно? Если D=0,то корень будет один,а в силу того,что квадратное уравнение относительно модуля ,то будет два ,а нам нужно 4

Находим корни квадратного уравнения и понимаем ,что 4 корня будет тогда ,когда модули будут равнять числу ,которое больше нуля ,если равно ,то |x|=0=>x=0 - одно решение

Осталось решить два простейших неравенства

Почему я убрал неравенство с плюсом?

Корень больше отрицательного числа при всех а,то есть ответом будет служить ОДЗ - подкоренное выражение больше или равно нуля ,но смотрим на вторую строчку ,мы уже написали это

Решаем второе неравенство и понимаем ,что при этих а будет ровно 4 решения

Минимальное целое а = - 28