Математика, вопрос задал 6Sinc , 1 год назад

Как это решить с помощью метода рационализации?

Приложения:

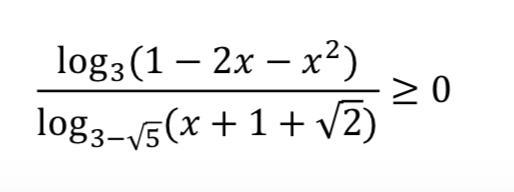
Ответы на вопрос

Ответил aastap7775

0

$\frac{log_3(1-2x-x^2)}{log_{3-\sqrt{5}}(x+1+\sqrt{2})}} \geq 0\\\frac{(3-1)(1-2x-x^2-1)}{(3-\sqrt{5}-1)(x+1+\sqrt{2}-1)} \geq 0\\\frac{-x(x-2)}{x+\sqrt{2}} \leq 0\\\frac{x(x-2)}{x+\sqrt{2}} \geq 0\\-----(-\sqrt{2})++++[0]----[2]++++++>x\\x \in (-\sqrt{2}; 0][2; +\infty)\\\left \{ {{1-2x-x^2 > 0} \atop {x+1+\sqrt{2} > 0 \atop {x+1+\sqrt{2} \neq 1}} \right.\\\left \{ {{x^2 + 2x - 1 < 0} \atop {x> -1 -\sqrt{2} \atop {x\neq-\sqrt{2}}} \right.$

$\left \{ {{(x-(-1+\sqrt{2}))(x-(-1-\sqrt{2})) < 0} \atop {x> -1 - \sqrt{2} \atop {x\neq-\sqrt{2}}} \right.\\\left \{ {{x \in (-1-\sqrt{2};-1+\sqrt{2})} \atop {x> -1 - \sqrt{2} \atop {x\neq-\sqrt{2}}} \right.\\x \in (-1-\sqrt{2};-\sqrt{2})(-\sqrt{2}; \sqrt{2} - 1)$

Объединяя с решением выше, получим:

$x \in (-\sqrt{2}; 0]$

Ответ: $x \in (-\sqrt{2}; 0]$

NNNLLL54: в 3 строчке описка: надо в числителе: -х(х+2)

Предыдущий вопрос

Следующий вопрос

Новые вопросы

Алгебра, 1 год назад

помогите пожалуйста срочно ...

Русский язык, 1 год назад

синтаксический разбор предложения А за ним шустрые синицы наблюдают ждут момента.

Математика, 1 год назад

Турист плыл на теплоходе 2целых 1/3ч по теченино реки, а 1,5 ч - по озеру. 3 Собственная скорость теплохода 32 км/ч. Скорость течения реки 2,2 км/ч. Какое расстояние проплыл турист за указанное время...

Английский язык, 1 год назад

помогите пожалуйста ...

Алгебра, 6 лет назад

У кошику 7 яблук, 10 бананів і 8 груш. Яка ймовірність того, що навмання обраний фрукт виявиться грушею?

Алгебра, 6 лет назад

Найдите значение приведенных ниже выражений, если: а)cos⁡ x; б)ctg⁡ x; в)sin ⁡2x.