К окружности радиуса 12 см проведены две касательные, образующие прямой угол. Прямая, проведенная через центр окружности, отсекает на одной стороне угла отрезок 28  см. Найдите длину отрезка, который отсекает эта прямая на другой стороне угла.
Помогите, пожалуйста!

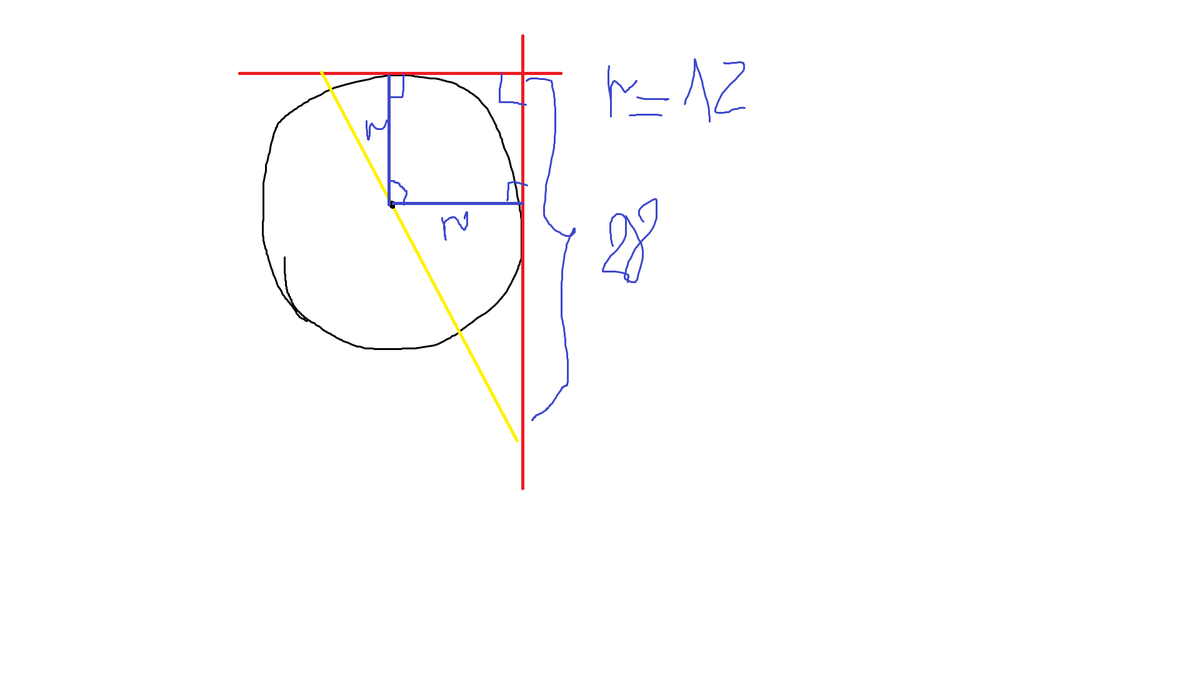
легко строим схему
А ТАМ УЖЕ СОСТАВЛЯЕМ ПРОПРЦИЮ
БОЛЬШИЙ ТРЕУГОЛЬНИК ИМЕЕТ ОСНОВАНИЕ 12 И КАТЕТ (28-12) ПО ТЕОРЕМЕ ПИФОГОРА.
ВТОРОЙ ТРЕГОЛЬНИК
ЭТО УЖЕ ПРОПОРЦИЯ БОКОВОЙ КАКТЕТ 12 : К (28-12) КАК ГИПОТИНУЗА К  Х  СКЛАДЫВАТЬ ОБЕ ГИПОТЕНУЗЫ И БУДЕТ ВСЯ ДЛИННА ЭТОГО ТРЕУГОЛЬНИКА.
Решение:
1 треугольник гипотинуза = корень из 16^2+12^2= 20
2 треугольник найдем пропорцию 12:16= х:20
х=15
самая большая гипотинуза тогда равна 15+ 20= 35