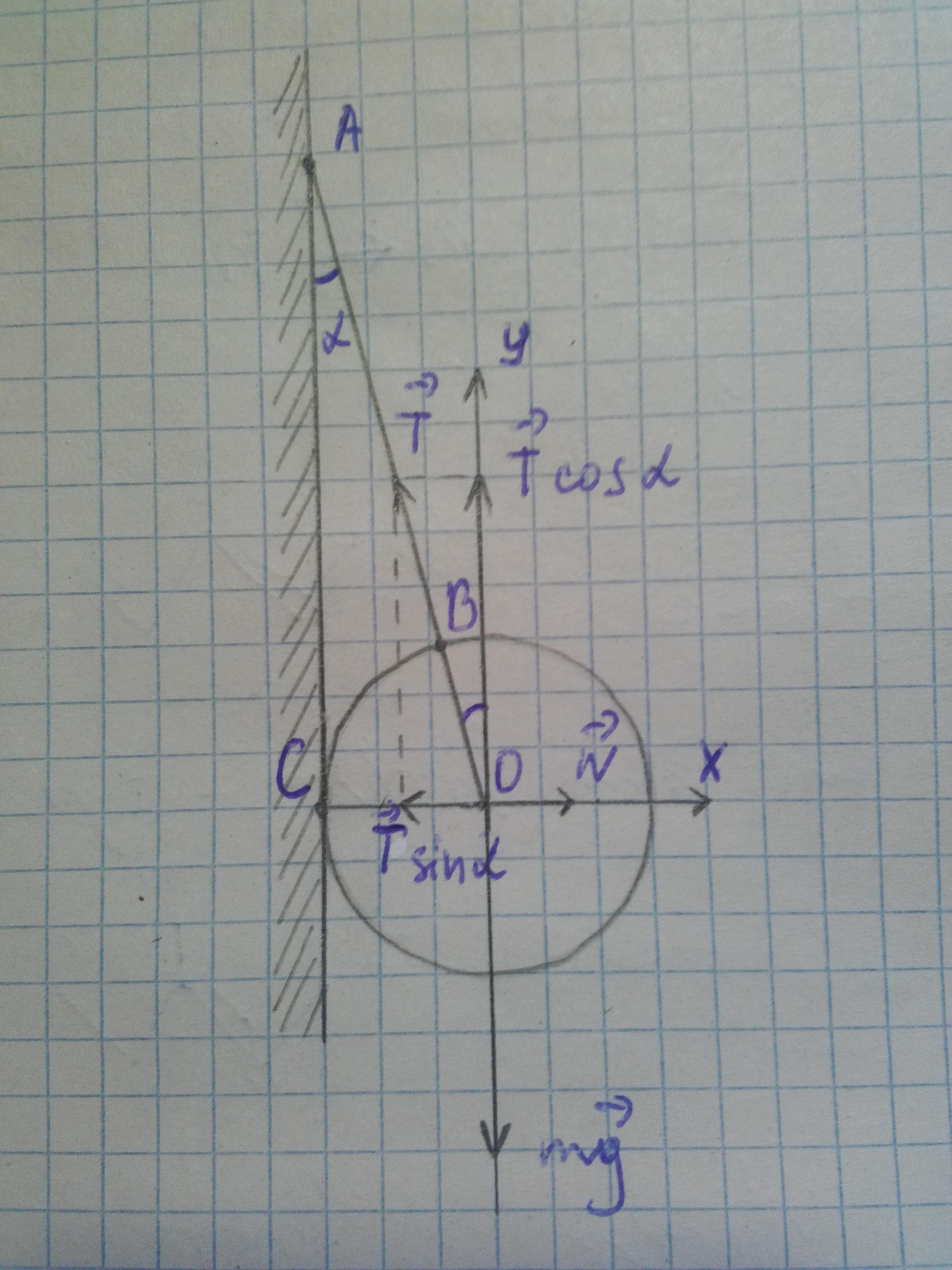
К гладкой вертикальной стене на нитке длиной 4 см подвешен шар массой 0,3 кг и радиусом 2.5см. Один конец нитки закреплен на стене, другой - на поверхности шара. Определить силу давления шара на стену.

Запишем второй закон Ньютона:
0=mg+T+N
На ось х:
 N=T*sinα
На ось у:

 mg=T*cosα

T=mg/cosα
____________
N=mg*sinα/cosα=mg*tgα
____________
Найдем расстояние от точки закрепления нити до точки касания шара с поверхность стены.
d²=(L+R)²-R²
d²=36
d=6см
_____________
tgα=R/d=2.5/6
_____________
N=0,3*10*2.5/6=2.5/2=1.25Н
Ответ:1.25Н 

Ответ: Н

Объяснение:

Дано:

см

кг

см

------------------------

Решение:

( см. рисунок )

см

см

Как видно на рисунке сила  давления шара на стену не обозначена это связано с тем что ее обозначение на рисунке может вызвать ряд неточностей, однако согласно 3 закону Ньютона  поэтому ее численное значение мы конечно же определить сможем. Со знаком + или - будет у нас зависит от выбранной системы отсчета ( поэтому формально )

Теперь согласно 1 и 2 закону составим систему

Отсюда

Согласно теореме Пифагора

Поэтому

Значит

Н

( сантиметры сократились и ответ мы получили в Ньютонах )