Известно, что графики функций 

y = x^ 2 + p  и  y = 2x − 2  имеют ровно одну общую точку. Определите координаты этой точки. Постройте графики заданных функций в одной системе координат.

 

1 способ:
{y=x²+p
{y=2x-2
x²+p=2x-2
x²-2x+2+p=0
D=(-2)²-4*1*(2+p)=4-8-4p=-4-4p
Для того, чтобы уравнение имело 1 решение, дискриминант должен быть равен 0, значит:
-4-4р=0
-4р=4
р=-1
     {y=x²-1
     {y=2x-2 
     x²-1=2x-2
     x²-1-2x+2=0
     x²-2x+1=0
     x₁+x₂=2
     x₁*x₂=1
     x₁=1
     x₂=1
        x=1
        y=x²-1=1-1
        y=0
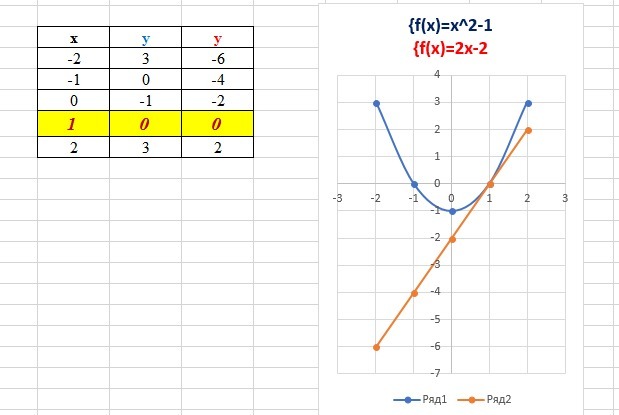
Точка пересечения графиков:  (1;0)
2 способ:
y=x²+p - парабола, у=2х-2 - касательная к параболе
Производная в точке х₀ равняется угловоvу коэффициэнту касательной
f`(x)=2x => 2x=2 => x=1
 касательная - в точке  х₀=1
f(x)=x²+p
f(x₀)=f(1)=1+p
f`(x)=2x
f`(x₀)=f`(1)=2
Уравнение касательной y=f`(x₀)*(x-x₀)+f(x₀):
y=2*(x-1)+(1+p)
y=2x-2+1+p
y=2x-1+p
Уравнение каcательной дано: у=2х-2, значит:
2х-1+р=2х-2
p=2x-2-2x+1
p=-1
1²-1=0
2*1-1=0
     Точка пересечения (1;0)

График во вложении